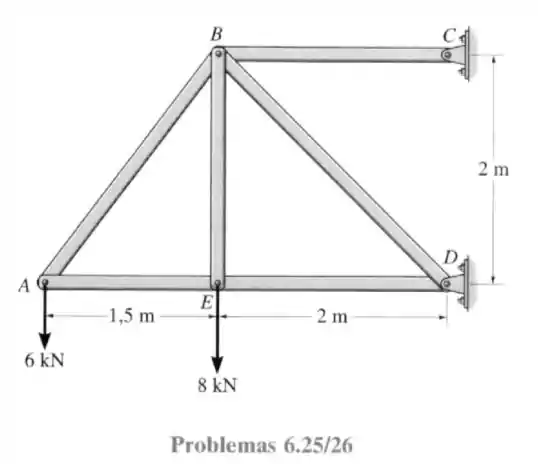
26- Cada elemento da treliça é uniforme e tem massa por unidade de comprimento de . Remova as cargas externas de e e determine a força aproximada em cada elemento devido ao peso da treliça. Indique se esses elementos estão sob tração ou compressão. Solucione o problema admitindo que o peso de cada elemento pode ser representado com uma força vertical, metade da qual é aplicada a extremidade de cada elemento.
Passo 1
Para começar a fazer esse exercício temos que entender muito bem o que se é dito na última frase do problema. Cada barra tem o peso distribuído igualmente nas duas extremidades de modo que temos a seguinte estrutura explodida abaixo.
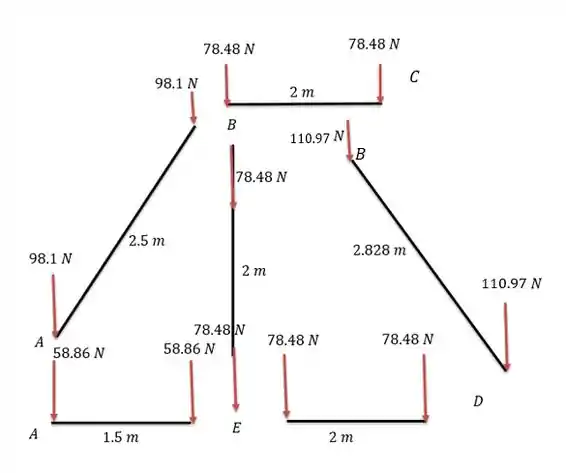
Calculo da força peso para uma barra.
Onde é a massa por unidade de comprimento que vale , logo para uma barra de m a força peso seria de:
Como ela estará nas duas extremidades, logo cada extremidade terá
Agora juntando todas as barras teremos o seguinte carregamento na estrutura.
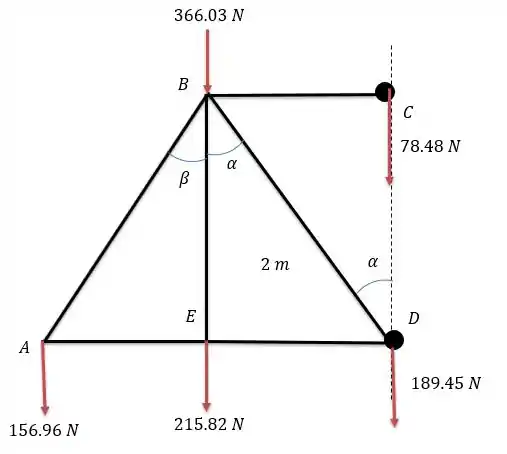
Sabendo da questão passada que os valores de e valem:
Passo 2
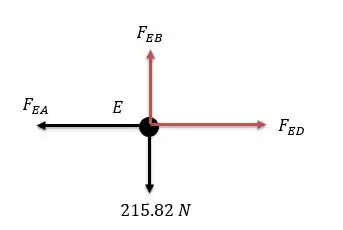
Agora podemos analisar nó a nó e ir anotando os valores da força em cada barra. Vamos começar pelo nó .
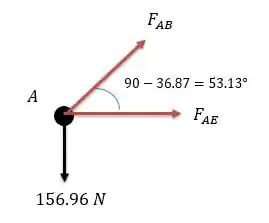
Pela somatória das forças verticais temos:
Força trativa.
E fazendo a somatória das forças horizontais:
Força compressiva.
Passo 3
Agora indo para o ponto .
Fazendo a somatória das forças verticais nesse ponto:
E fazendo a somatória das forças horizontais:
Passo 4
Agora para finalizar vamos para o ponto (ir para o ponto ou pode ser um pouco chato pois aí teríamos que calcular as reações tal como fizemos na questão passada).
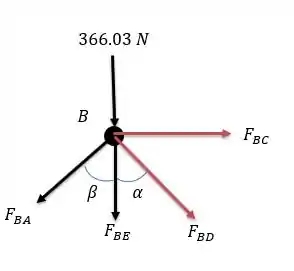
Fazendo a somatória das forças verticais:
Força compressiva.
E para a somatória das forças horizontais:
Força trativa.