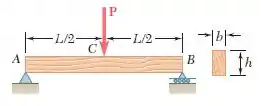
19 Uma viga de madeira de comprimento e seção transversal retangular suporta uma única força concentrada em seu ponto médio C. (a) Mostre que a relação dos valores máximos das tensões de cisalhamento e normal na viga é igual a , em que e são, respectivamente, a altura e o comprimento da viga. (b) Determine a altura h e a largura b da viga, sabendo que L=2m, P= 40 kN, e .

Vamos fazer o diagrama de corpo livre:

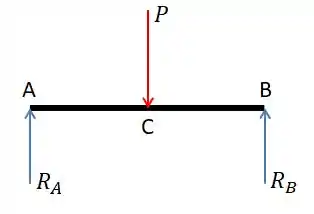
Acho que é um pouco intuitivo a gente achar que , né??? Mas vamos fazer o somatório das forças em y:

E também o de momento (considerando o sentido anti-horário positivo):

Substituindo no balanço de força:

E realmente . Nossa intuição ta boa, heim.

Vamos fazer o Diagrama de Esforço Cortante: (pra uma carga localizada)

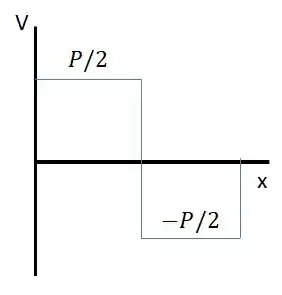
Daí conseguimos tirar que:

E o diagrama de momento fletor:

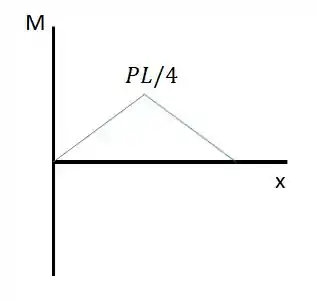
Que podemos tirar que:

Agora que já temos tudo, podemos só calcular:

E também:

Dividindo os dois:

Para letra (b) vamos usar as equações que já achamos, né... (tomando suuuper cuidado com as unidades, heim)

E já vamos começar achando h, usando:

E pra achar o b:

E acabamos... Ufaaa... vamos pra próxima??