Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.9 - Ex. 193

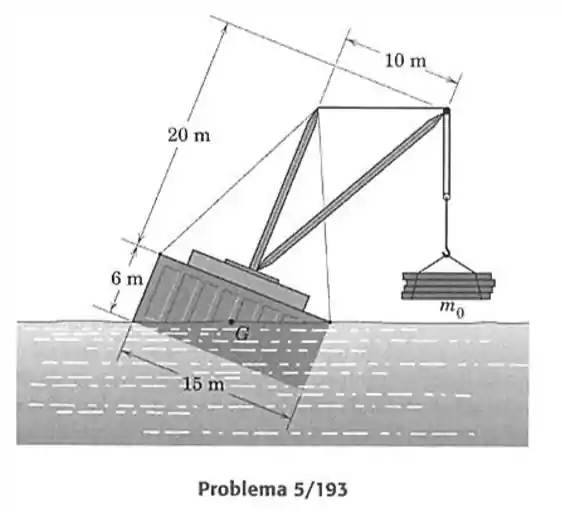
193- A balsa guindaste tem uma seção transversal retangular de 6   m por 15   m ao longo de todo o seu comprimento de 40   m . Se a submersão e a adernagem máximas permissíveis na água do mar são representadas pela posição mostrada, determine a máxima massa segura m 0 correspondente que a balsa pode manejar na posição estendida de 10   m do guindaste. Ache, também, o deslocamento total m em toneladas métricas da balsa sem carga. A distribuição dos equipamentos e do lastro coloca o centro de gravidade G da balsa, desconsiderando a massa m 0 , no centro do casco.

Passo 1

A balsa pode ser desenhada da seguinte forma:

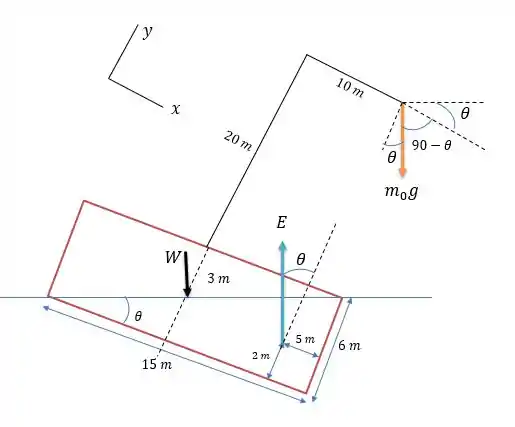
O valor de θ pode ser encontrado pelo triângulo retângulo formado:

t g   θ = 6 15 → θ = 21.8

O empuxo será proporcional a área do prisma formada pelos catetos de 6   m e 15   m , logo na água salgada o empuxo será:

E = 1030 × 9.81 × 6 × 15 × 40 2 = 18.188 × 10 6

Passo 2

Fazendo a somatória dos momentos no centro de massa do container e o empuxo na vertical e na horizontal em relação aos eixos normais ao container.

∑ M W = 0

- E c o s   θ × 7.5 - 5 + E s i n   θ 3 - 2 + m 0 g c o s   θ × 10 + m 0 g s i n   θ × 23 = 0

Sempre em relação ao centro de gravidade.

E ( sin ⁡ θ - 2.5 cos ⁡ θ ) = - m 0 g ( 10 cos ⁡ θ + 23 sin ⁡ θ )

m 0 = E ( 2.5 cos ⁡ θ - sin ⁡ θ )   9.81 ( 10 cos ⁡ θ + 23 sin ⁡ θ )

m 0 = 203 × 10 3   k g

Passo 3

Agora podemos fazer a somatória das forças verticais no sistema para encontrar a massa do container:

W + m 0 g = E

9.81 m + 203 × 10 3 × 9.81 = 18.188 × 10 6

m = 1651.03 × 10 3   k g

Resposta

m 0 = 203 × 10 3   k g

m = 203 × 10 3   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse F 1 , F 2 e F 3 como vetores cartesianos.
Determine as componentes x e y de cada força que atua sobre a chapa de fixação de uma treliça de ponte. Mostre que a força resultante é zero.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Determine a intensidade e a direção θ da força resultante F R . Expresse o resultado em termos das intensidades das componentes F 1 e F 2 e do ângulo ϕ .
Expresse cada uma das três forças que atuam sobre o suporte na forma vetorial cartesiana e determine a intensidade da força resultante e sua direção, medida no sentido horário a partir do eixo x posit