Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 65
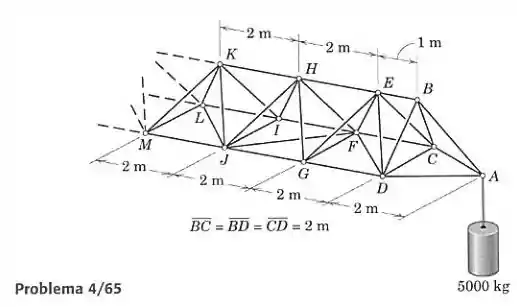
A lança comprida de uma grua de construção, da qual uma parte é mostrada, é um exemplo de uma estrutura periódica composta por unidades estruturais iguais e repetidas. Use o método das seções para encontrar as forças nos elementos e .
Passo 1
Como queremos utilizar o método das seções, faremos um corte na treliça espacial, passando um plano pelos elementos , , , , e . A parte que sobra é então mostrada:
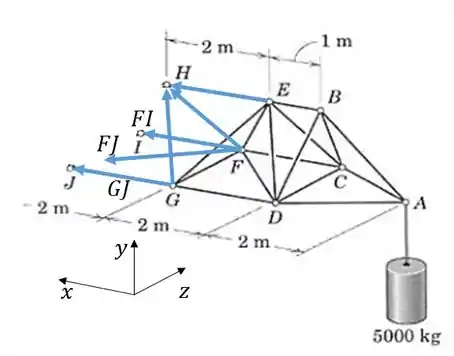
Temos 3 forças que não passam por , incluindo as duas que queremos encontrar. Fazendo a equação de momento em torno de , então só aparecerão essas 3 forças como incógnita, e conseguiremos resolver o sistema.
Passo 2
Vamos primeiro colocar as forças na forma módulo vezes vetor unitário. Para os eixos escolhidos, temos:
Passo 3
Agora, Agora vamos calcular o momento causada por cada uma das forças dos 3 elementos e pela massa de 5000 kg. Primeiro para . A angulação das barras em relação a horizontal quando olhadas perpendicularmente ao eixo é de 60°. O vetor que liga a é então:
E de para :
Calculamos então os momentos feitos pelas três forças das barras. Primeiro :
Agora para :
E para :
Por último, calculamos o momento realizado pela massa de 5000 kg. O momento é positivo em torno do eixo :
Passo 4
Pelo equilíbrio, a soma de todos os momentos deve ser zero:
Separando as componentes:
Da primeira equação, tiramos que:
Da segunda, como :
Da terceira:
Como e :
O valor negativo indica que a força é de compressão, e não de tração como indicamos.