Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.4 - Ex. 48

48- Se θ = 60 ° e F = 20   k N , determine a intensidade da força resultante e sua direção, medida no sentido horário, a partir do eixo x positivo.

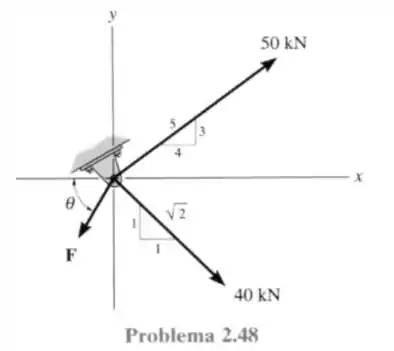
Passo 1

Substituindo os valores dados no enunciado temos o seguinte sistema de forças.

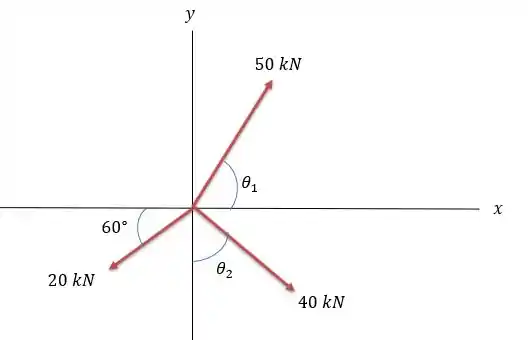
Onde o valor de cosseno e seno dos ângulos θ 1 e θ 2 são iguais a:

cos ⁡ θ 1 = 4 5 ;   sin ⁡ θ 1 = 3 5

sin  θ 2 = cos ⁡ θ 2 = 1 2   = 2 2

Pois:

cos ⁡ θ = c a t e t o   a d j a c e n t e h i p o t e n u s a

sin ⁡ θ = c a t e t o   o p o s t o   h i p o t e n u s a

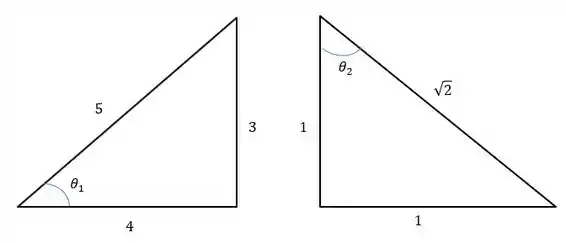
Passo 2

Agora fazendo a somatória das forças em x temos:

F x = - 20 cos ⁡ 60 + 50 cos ⁡ θ 1 + 40 sin ⁡ θ 2   k N

F x = - 10 + 50 × 4 5 + 40 × 2 2 = 58.28   k N

Agora fazendo a somatória das forças em y temos:

F y = 50 sin ⁡ θ 1 - 20 sin ⁡ 60 - 40 cos ⁡ θ 2   k N

F y = 50 × 3 5 - 20 s i n   60 - 40 × 2 2 = - 15.6   k N

Passo 3

Com isso a força resultante será igual a:

F r = F x 2 + F y 2 = 58.28 2 + - 15.6 2   k N = 60.33   k N

E a angulação medida no sentido horário será igual a:

θ = - tan - 1 ⁡   - 15.6 58.28 = 14.98 °

Resposta

F r = 60.33   k N

θ = 14.98   °

Ver Outros Exercícios desse livro