Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 22.Problemas - Ex. 21

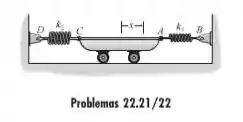
21. O carrinho tem uma massa de m e está fixado a duas molas, cada uma tendo uma rigidez k 1 = k 2 = k , comprimento não deformado de l 0 ,   e um comprimento deformado de l quando o carrinho está na posição de equilíbrio. Se o carrinho é deslocado por uma distâmcia de x = x 0 de tal maneira que ambas as molas permanecem em tensão ( x 0 < l - l 0 ) , determine a frequência natural de oscilação.

Passo 1

Sabemos que a força elástica é dada por :

F e l = k x

Neste caso:

x A B = l - l 0 - x

x A C = l - l 0 + x

Passo 2

Aplicando a segunda lei de Newton para situação em questão, podemos escrever:

∑ F x = m a x

k l - l 0 - x - k l - l 0 + x = m x -

- 2 k x = m x -

x - + 2 k m x = 0

Passo 3

Comparando a Edo acima, podemos a partir do resultado da mesma dizer que frequência natural de oscilação é dada por:

ω B = 2 k m    

Resposta

ω B = 2 k m    

Ver Outros Exercícios desse livro