Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 126

Uma corda está enrolada em torno da bobina interna da engrenagem. Se ela é puxada com uma velocidade constante v, determine as velocidades e acelerações dos pontos A e B. A engrenagem rola sobre a cremalheira fixa.

Passo 1

Começaremos o exercício analisando a velocidade do sistema conforme o diagrama a seguir:

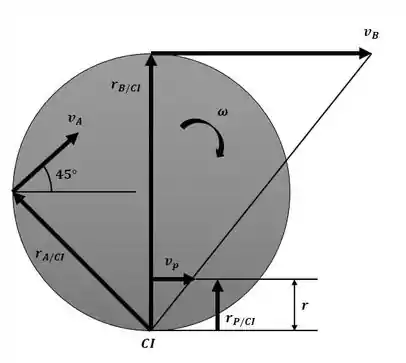
A velocidade angular da engrenagem é dada por:

ω = v r

A velocidade no ponto B é dada por:

v B = ω r B / C I = v r 4 r → v B = 4 v

A velocidade no ponto A é dada por:

v A = ω r A / C I = v r ( 2 r 2 + 2 r 2 → v A = 2 2 v

Passo 2

Antes de aplicarmos a equação da aceleração, devemos notar que a G = 0 e α = 0 , sendo assim:

r B / G = 2 r j →

r A / G = - 2 r i →

Passo 3

Agora iremos aplicar a equação da aceleração entre os pontos B e G com o auxílio da figura a seguir:

a → B = a → G + α × r → B / G - ω 2 r → B / G

a → B = 0 + 0 - v r 2 2 r j → → a → B = - 2 v 2 r j →

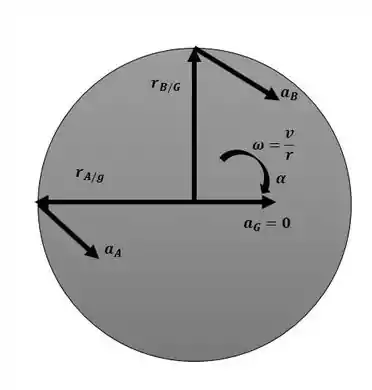
Agora aplicando a equação da aceleração para os pontos A e G:

a → A = a → G + α × r → A / G - ω 2 r → A / G

a → A = 0 + 0 - v r 2 - 2 r i → → a → A = 2 v 2 r i →

Resposta

v A = 2 2 v

a → A = 2 v 2 r

v B = 4 v

a → B = - 2 v 2 r j →

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 pol./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante de ω 2 = 1.5r a d/ s em relação ao braço CD.
Dois discos, cada um com raio de 130 mm, são soldados à haste CD de 500 mm. A unidade de haste e discos gira a uma taxa constante ω 2 = 3 r a d / s em relação ao braço AB. Sabendo que no instante most
No problema 15.244, determine a velocidade e aceleração do (a) Ponto G, (b) Ponto H15.244 Dois discos, cada um com raio de 130 mm, são soldados à haste CD de 500 mm. A unidade de haste e discos gira a
A placa vertical mostrada é soldada ao braço EFG e toda a unidade gira a uma taxa constante ω 1 = 1.6 r a d / s em torno do eixo Y. Ao mesmo tempo, uma correia de elos contínua se move ao redor do per
A placa vertical mostrada é soldada ao braço EFG e a unidade inteira gira a uma taxa constante ω 1 = 1.6 r a d / s em torno do eixo Y. Ao mesmo tempo, uma correia de elo contínua se move ao redor do p