Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 1
Determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido horário a partir do eixo x.
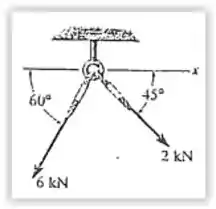
Passo 1
Esse probleminha pede a força resultante aplicada então vamos decompor as duas forças nos eixos e e somar.
Vamos ver no que da?
Passo 2
Vamos começar calculando as forças no eixo x.
Vamos definir nossas forças e nossas componentes.
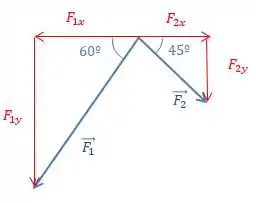
Sendo assim, teremos:
O sinal negativo em surge pelo sentido da força, que está para a esquerda. (esse sentido é uma mera convenção).
Tem que lembrar que utilizamos cosseno quando a componente que queremos está “colada” no ângulo. Olha como a horizontal ta colada nos dois ângulos.
Somando essas forças temos:
Passo 3
Agora vamos fazer a mesma coisa com o eixo vertical :
Aqui os sinais negativos aparecem porque as forças estão voltadas para baixo. (Repare que convencionamos o sentido positivo para cima e para a direita).
Nesse caso usamos o seno, pois quando a componente está “separada” do ângulo, usamos o seno. Olha como a componente vertical dessas forças ficaria separadas do ângulo.
Somando:
Passo 4
Beleza! Agora como vamos saber o ângulo dessa força? Que é o que o problema pede. Primeiro vamos fazer um esqueminha.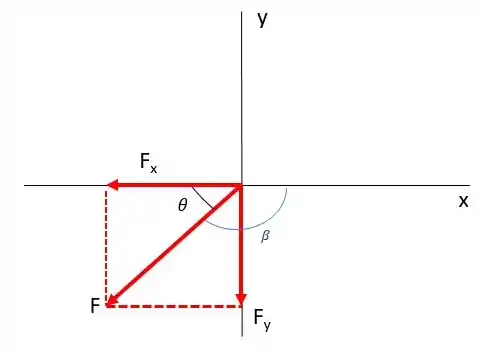
O que queremos é o ângulo que é o ângulo medido a partir do eixo positivo no sentido horário.
Para achar esse ângulo, a gente pode primeiro encontrar o ângulo , usando trigonometria:
Note que utilizamos o módulo porque o sentido, agora, não faz diferença.
Agora vamos calcular o arcoss para achar o valor do ângulo:
E como queremos o ângulo daquele desenho, vamos ter:
E para fechar, só precisamos do módulo dessa força, olhando para o desenho acima, esse módulo nada mais é do que a hipotenusa do nosso triângulo :o
Então, vamos aplicar pítagoras...