Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 43

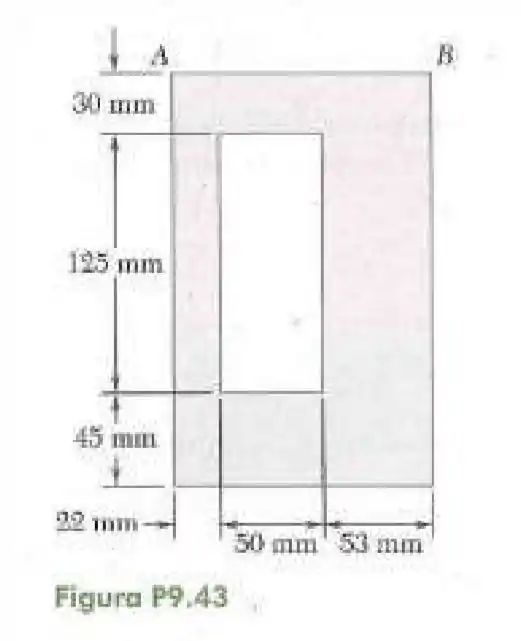
43- Determine os momentos de inércia I x e I y da superfície mostrada na figura em relação aos eixos centroidais paralelo e perpendicular ao lado A B , respectivamente.

Passo 1

Para fazer essa questão nós precisamos descobrir a posição do centro de gravidade do corpo todo, sabendo que podemos dividir esse corpo em

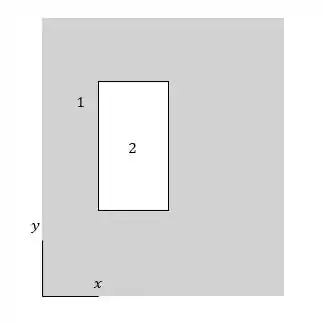
Sabendo que 1 é o retângulo todo de comprimento igual a 125   m m e altura igual a 200   m m e a região 2 somente o furo.

As coordenadas do centro do corpo serão iguais a:

x ¯ = ∑ x A ∑ A ;     y ¯ = ∑ y A ∑ A

Ou seja:

x ¯ = x 1 ¯ A 1 - x 2 ¯ A 2 A 1 - A 2 ;     y ¯ = y 1 ¯ A 1 - y 2 ¯ A 2 A 1 - A 2

Dessa forma temos:

Dessa forma:

x ¯ = 1562500 - 293750 25000 - 6250 = 67.67   m m

y ¯ = 2500000 - 671875 25000 - 6250 = 97.5   m m

Passo 2

Dessa forma a inércia no eixo x será dada por:

I x = I 1 x - I 2 x

E a inércia dos dois retângulos serão calculados da seguinte forma:

I x = b h 3 12 + A d 2

Onde d agora é a distância em y pro centro de gravidade do corpo todo.

Nós teremos:

I 1 x = 125 × 200 3 12 + 125 × 200 100 - 97.5 2 = 83.49 × 10 6   m m 4

I 2 x = 50 × 125 3 12 + 50 × 125 107.5 - 97.5 2 = 8.76 × 10 6   m m 4

Logo:

I x = 74.73 × 10 6   m m 4

Passo 3

E a inércia em y será dada por:

I y = I 1 y - I y 2

E a inércia nos retângulos serão iguais a:

I y = b 3 h 12 + A d 2

Onde d agora é a distância em x pro centro de gravidade do corpo todo.

Logo:

I 1 y = 125 3 × 200 12 + 125 × 200 67.67 - 62.5 2 = 33.22 × 10 6   m m 4

I 2 y = 50 3 × 125 12 + 50 × 125 67.67 - 47 2 = 3.97 × 10 6   m m 4

Logo a inércia em y será:

I y = 29.25 × 10 6   m m 4

Resposta

I x = 74.73 × 10 6   m m 4

I y = 29.25 × 10 6   m m 4

Ver Outros Exercícios desse livro