23. O alvo de 3kg desliza livremente ao longo das guias horizontais lisas BC e DE, as quais estão ´´ encaixadas´´ em molas que têm, cada uma, rigidez . Se uma bala de 60g é atirada com uma velocidade de 900 m/s e se embute no alvo, determine a amplitude e frequência de escilacao do alvo.
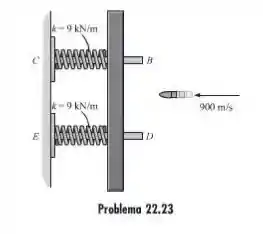
Passo 1
Aplicando a conservação do momento linear:
Passo 2
Como estamos diante de um arranjo com duas molas em paralelos, temos que a constante elástica equivalente é dada por:
A partir daí podemos calcular a frenquência angular do sistema como:
Passo 3
A equação que descreve a oscilação do sistema é:
Quando
Como . Substituindo na equação obtemos:
Passo 4
Derivando a equação acima com relação ao tempo:
Aqui, quando Substituindo na equação vem: