Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 80

80. Se a engrenagem interna D gira no sentido anti-horário com uma velocidade angular ω D = 5 r a d s enquanto a barra de ligação AB gira no sentido horário com uma velocidade angular ω A D = 10   r a d / s , determine a velocidade angular da engrenagem C.

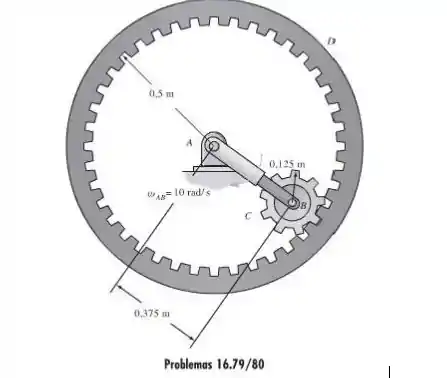
Passo 1

A velocidade do centro B da engrenagem C e do ponto de contatoo P podem ser determinadas como:

v B = ω A B r A B = 10 0,375 = 3,75   m / s

v P = ω D r P = 5 0,5 = 2,5   m / s

Passo 2

Como nesse caso a engrenagem externa não está parada. Aplicando a equação da velocidade relativa entre o ponto de contato e o centro B, teremos:

v B = v P + ω C × r B / P

- 3,75 i = 2,5 i + ω C k × 0,125 j

- 3,75 i = ( 2,5 - 0,125 ω C ) i

Então,

- 3,75 = 2,5 - 0,125 ω C

ω C = 50   r a d / s

Resposta

ω C = 50   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

16.93. Se a extremidade A do cilindro hidráulico está se deslocando com uma velocidade V A = 3 m / s , determine a velocidade angular da barra B C no instante mostrado.
No instante mostrado, o caminhão se desloca para a direita de 3m / s , enquanto o tubo rola no sentido anti-horário a ω = 6r a d / s sem deslizar em B. Determine a velocidade do centro G do tubo.
16.91. Se é dada uma velocidade V o = 10m / s ao centro O da engrenagem, determine a velocidade do bloco deslizante B no instante mostrado.
16.96. Se C tem uma velocidade V C = 3 m / s , determine a velocidade angular da roda no instante mostrado.
16.89. Se o segmento C D tem uma velocidade angular ω C D = 6 r a d s , Determine a velocidade do ponto E no segmento B C e a velocidade angular do segmento A B no instante mostrado.