Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 23
23- Determine por integração direta o momento de inércia polar da superfície mostrada na figura em relação ao ponto . Usando o resultado do item , determine os momentos de inércia da área dada em relação ao eixo .
Passo 1
O momento de inércia polar tem esse nome por conta da variável das coordenadas polares, e ela é calculada da seguinte forma:
E para calcular o momento inercial no eixo não escolhemos uma linha horizontal para calcular o elemento de área do corpo, na inércia escolhemos uma corpo anelar de espessura que nos diz o elemento de área desse corpo da seguinte forma:
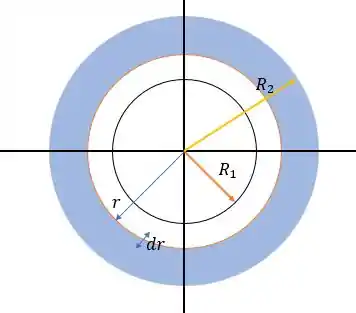
De tal forma que essa superfície anelar tem um elemento de área igual a:
Pois a derivada da área de um círculo é o comprimento do mesmo.
Passo 2
Dessa forma a inércia polar valerá:
Onde varia de até
Passo 3
Por simetria podemos dizer que:
Isso é temos a mesma área acima do eixo igual a mesma área a direita do eixo .
E como :
Então:
Logo: