Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 22.Problemas - Ex. 25

25. A barra delgada de massa m é suportada por duas cordas de igual comprimento. Se ela é submetida a um deslocamento angular pequeno θ em torno do eixo vertical e solta, determine o período natural de oscilação.

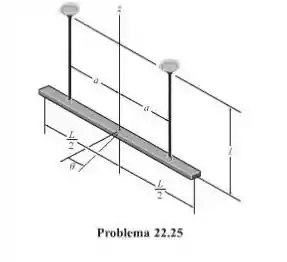
Passo 1

Aplicando a segunda lei de Newton na direção z:

∑ F z = m a Z

2 T cos ⁡ ϕ - m g = 0

T = m g 2 cos ⁡ ϕ

Então,

∑ F z = \ I Z α

- 2 m g 2 cos ⁡ ϕ sin ⁡ ϕ α = 1 12 m L 2 θ ¨

θ ¨ + 12 g a L 2 tan ⁡ ϕ = 0

Para um ângulo θ muito pequeno, temos da geometria:

I ϕ = α θ

ϕ = α I θ

Substituindo na equação:

θ ¨ + 12 g a L 2 tan ⁡ α I θ = 0

Para um ângulo θ muito pequeno, temos da geometria:

tan ⁡ ϕ α I θ ≈ α I θ

Então,

θ ¨ + 12 g a 2 L 2 I θ = 0

Passo 2

Comparando a equação acima com a equação padrão existente ao longo da seção:

ω n = 12 g a 2 L 2 I = a L 12 g I

Passo 3

O período natural de oscilação é:

τ = 2 π ω n = 2 π L a l 12 g

Resposta

τ = 2 π L a l 12 g

Ver Outros Exercícios desse livro