Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 93
16.93. Se a extremidade do cilindro hidráulico está se deslocando com uma velocidade = 3 , determine a velocidade angular da barra no instante mostrado.
Passo 1
Separando a estrutura em duas para melhor compreensão do problema, aqui temos a haste , agora iremos definir a rotação sobre um eixo fixo. Fig. a.
Como sabemos, a velocidade linear de um segmento qualquer, é dada em função da seguinte relação:
. (0,4)
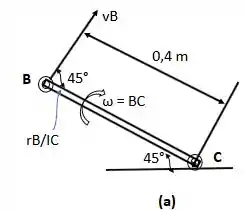
Passo 2
Podemos determinar também intersecção dos segmentos de linha , através do ângulo que nos foi dado, ou seja:
=
=
=
Passo 3
Movimento plano geral: A localização do para a haste é indicada na Fig. b. a partir da geometria mostrada nesta figura, obtemos o o valor da intersecção dos segmentos de linha pela relação :
=
=
=
Passo 4
Assim, a velocidade angular da haste AB pode ser determinada a partir da velocidade em A e da intersecção deste mesmo ponto em relação a :
= 5,303
Passo 5
Como a velocidade angular da haste no nosso primeiro passo era uma das duas incógnitas da equação, podemos agora, determinar a velocidade angular da haste .
=
. (0,4) = 5,303 . (0,4)
= 5,30
Resposta
= 5,30