Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 27

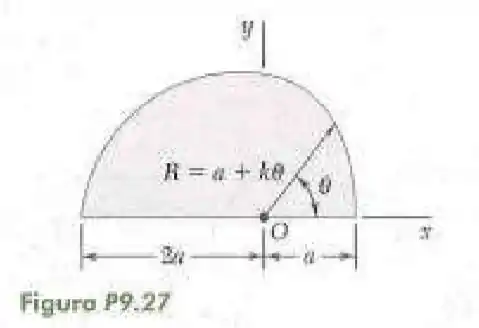
27- Determine o momento de inércia polar e o raio de giração polar da superfície sombreada mostrada na figura em relação ao ponto O .

Passo 1

Vamos encontrar a constantes k sabendo que quando θ = π o valor de r será igual a 2 a .

Logo:

2 a = a + k π

k = a π

Logo a equação polar dessa superfície será:

r = a + a θ π

Passo 2

Agora podemos fazer o momento de inércia polar sabendo que ela terá equação igual a:

J = ∫ r 2   d A

Onde d A = r   d r   d θ pois tanto r varia em função de θ não sendo possível pegar uma superfície anelar como fizemos na questão anterior. r vai de 0 até a equação encontrada e θ vai de 0 até π . Dessa forma:

J = ∫ 0 π ∫ 0 a + a θ π r 2   ( r   d r   d θ ) = ∫ 0 π ∫ 0 a + a θ π r 3   d r   d θ  

Fazendo essa integral nós temos:

J = ∫ 0 π r 4 4 0 a + a θ π   d θ

J = a 4 4 ∫ 0 π 1 + θ π 4 d θ

Fazendo a substituição u = 1 + θ π , nós teremos d u = 1 π   d θ

π d u = d θ

Dessa forma:

π ∫ u 4 d u = π u 5 5

Aplicando isso na integral no domínio de θ nós teremos

J = a 4 4 π 5 1 + θ π 5 0 π

Aplicando esse intervalo nós temos:

J = a 4 π 20 2 5 - 1 = 31 a 4 π 20

Passo 3

Agora para encontrar o raio de giro polar basta encontrar a área e para isso só basta integrar o elemento de área que encontramos:

d A = r   d r   d θ

A = ∫ 0 π ∫ 0 a + a θ π r   d r   d θ

A = ∫ 0 π r 2 2 0 a + a θ π   d θ

Isso será o mesmo que:

A = a 2 2 ∫ 0 π 1 + θ π 2 d θ

Para resolver essa integral precisamos fazer a substituição:

u = 1 + θ π

d u = d θ π → π d u = d θ

Logo:

π ∫ u 2   d u = u 3 π 3

Aplicando esse resultado na integral própria nós temos:

A = a 2 2 π 3 1 + θ π 3 0 π

Aplicando o intervalo teremos:

A = π a 2 6 2 3 - 1 = 7 π a 2 6

Passo 4

Dessa forma o raio de giro será:

k = J A

k = 31 a 4 π 20 7 π a 2 6 = a 93 7 0

Resposta

J = 31 a 4 π 20

k = a 93 7 0

Ver Outros Exercícios desse livro