Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 61
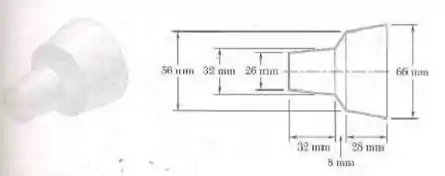
O quebra-luz de alumínio de uma pequena luminária de alta intensidade tem espessura uniforme de . Sabendo que a densidade do alumínio é de , determine a massa do quebra-luz.
Passo 1
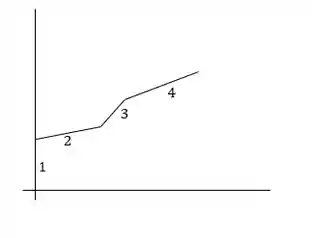
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine a massa do quebra-luz. Para isso, vamos utilizar o teorema de Pappus para Área a fim de encontrarmos a massa. Primeiro, vamos dividir a vista frontal da nossa figura. Fica assim:
Passo 2
Depois, precisamos encontrar a distância do centroide do comprimento para o eixo de rotação. Temos:
Assim como o comprimento das linhas:
Passo 3
Por fim, vamos usar a fórmula do teorema de pappus para corpos compostos:
Agora, basta substituirmos na fórmula da massa:
Resposta
Exercícios de Livros Relacionados
Determine por integração direta o centroide da área mostada na figura. Demonstre sua resposta em termos de a e b .
Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e b .
Determine por integração direta o centroide da área a seguir. Determine sua resposta em termos de a e h .
Determine as coordenadas do centroide por integração em termos de a e b :
Determine por integração direta o centroide da área mostrada na figura.