Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 60
Três diferentes perfis de correia de acionamento devem ser estudados. Se em todas as situações cada correia fizer contato com metade da circunferência de sua polia, determine a área de contato entre correia e polia para cada projeto.
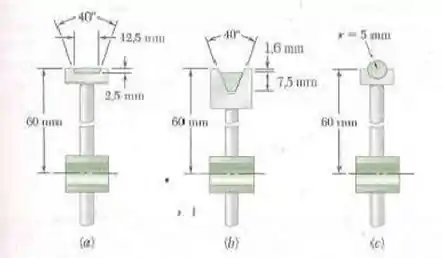
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine a área de contato entre correia e polia em três situações. Para isso, vamos utilizar o teorema de pappus. Para a primeira, temos:
Passo 2
Agora é só repetirmos o processo para o segundo e para o terceiro:
E para o terceiro:
Resposta
Exercícios de Livros Relacionados
Determine por integração direta o centroide da área mostrada na figura.
Determine as coordenadas do centroide por integração em termos de a e b :
Um arame homogêneo é dobrado na forma mostrada na forma a seguir. Determine por integração direta a coordenada x de seu centroide.
Um furo de 19m m de diâmetro é feito em uma peça de aço de 25m m de espessura. Em seguida, o furo é escareado como mostrado na figura. Determine o volume de aço removido durante o processo de escaream
Um arame homogêneo é dobrado na forma mostrada na forma a seguir. Determine por integração direta a coordenada x de seu centroide.