Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 5.4 - Ex. 28
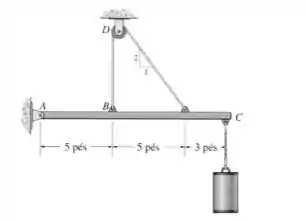
28. Determine a força no cabo e os componentes horizontal e vertical do pino em . A polia em é sem atrito e o cilindro pesa .
Passo 1
Fala galerinha, prontos pra mais uma de estática?
Primeiro, vamos ver o diagrama de forças da nossa situação, para analisar as reações que teremos que determinar no nosso sistema e ficar mãos simples de ver o que fazer.
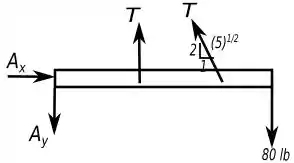
Como você pode reparar dos dois lados da corda a tração é a mesma já que temos a mesma corda, não faria sentido ser diferente.
Além disso, o triângulo desenhado junto com a força , veio da relação dada no desenho do enunciado, onde os catetos são dados por e e a hipotenusa, foi dada por pítagoras:
Então para achar as reações que o enunciado pede, teremos que usar as equações de equilíbrio.
Mas será mais conveniente calcular o momento em relação ao ponto , já quee , não interferem no cálculo do momento pois suas linhas de ação passam por .
Passo 2
Vamos então calcular o momento em relação a , para acharmos .
Considerando o sentido anti-horário como positivo, teremos:
Lembrando que temos que decompor a força T oblíqua em relação ao eixo y:
Passo 3
Agora vamos analisar as equações de equilíbrio referentes a força primeiro na direção , depois na direção .
Onde: