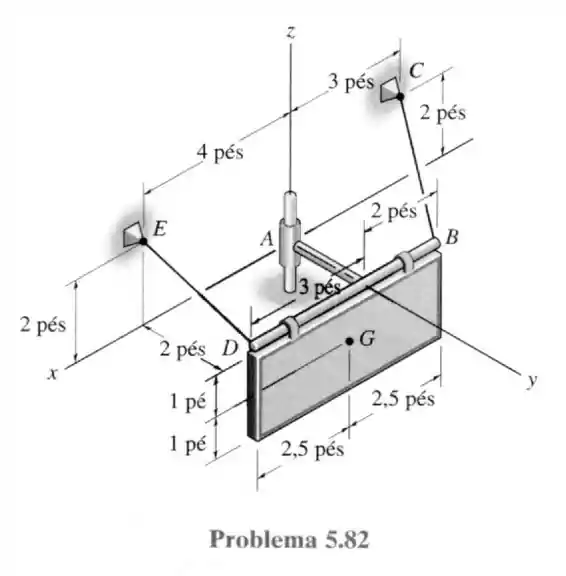
82- Determine as tensões nos cabos de reação que atuam no colar sem atrito em , necessários para manter a placa de em equilíbrio. O centro de gravidade da placa está em .
Passo 1
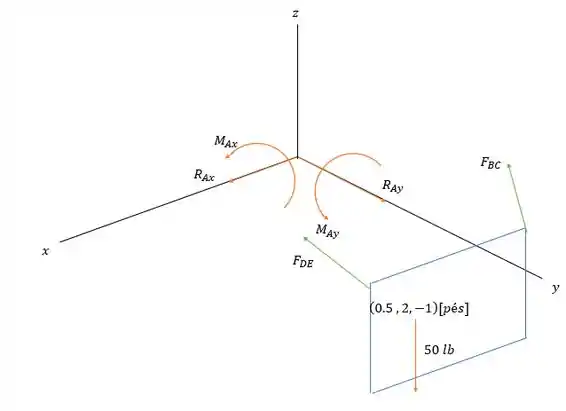
Esse colar em tem total movimento no eixo não oferecendo resistência a giro nem a movimento no eixo . Nos outros eixos temos total restrição de movimento e giro o que faz com que tenhamos o seguinte diagrama de forças.
Para resolver esse problema vamos escrever a representação vetorial dos dois cabos. Para isso vamos começar escrevendo a posição dos pontos extremos dos dois vetores.
A figura está mal desenhada! Imagine que o eixo entra na placa e está afastada de do eixo em e afastada de em do eixo . E a distância entre e o eixo de nos mostra que é um ponto pertencente ao plano , assim como .
Logo os vetores serão iguais a:
Onde o comprimento será igual a:
O que nos dá uma força vetorialmente representada como:
Agora o vetor fica como:
Que conseguimos ver que tem o mesmo comprimento de , logo a força será igual a:
Passo 2
Fazendo a somatória das forças em temos:
Agora a somatória das forças em :
E a somatória das forças em :
A primeira equação com a última nos mostra que:
Passo 3
Agora vamos calcular os momentos começando por :
Agora juntando com a equação
Temos:
Logo:
Logo será igual a:
Passo 4
Agora calculando os momentos em :
Agora a somatória dos momentos em :