90- O poste está sujeito as duas forças mostradas na figura. Determine os componentes de reação do apoio , admitindo ser uma junta esférica. Calcule também a tensão em cada um dos cabos de sustentação. e .
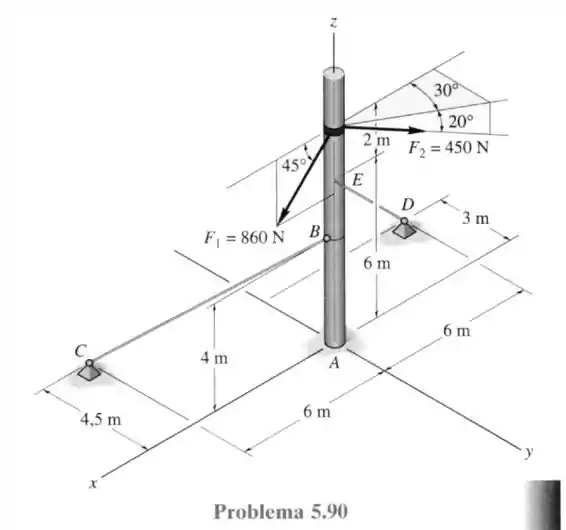
Passo 1
Por ser uma junta esférica na base nós sabemos que a junta apresenta reações verticais positivas em todos os eixos da seguinte forma que temos o seguinte diagrama de forças no poste.
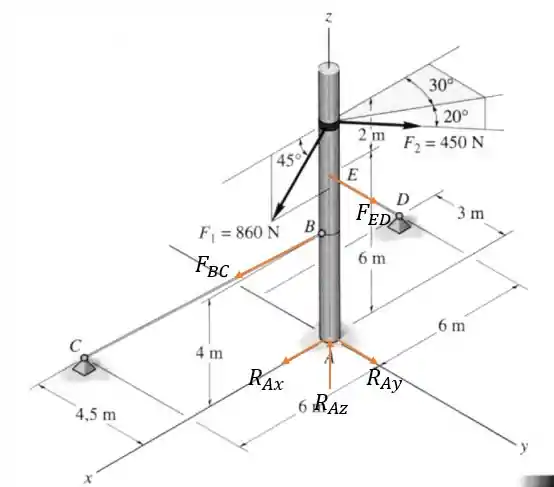
Para começar a resolver esse problema vamos vetorizar as forças que conhecemos e as forças nos cabos, começando por temos:
Agora vetorizando a força .
O que vale:
Agora precisamos vetorizar as forças nos cabos e . Para isso vamos descobrir as posições desses pontos:
Logo os vetores serão:
O comprimento dos dois vetores serão iguais a:
Isso faz com que o vetor das forças seja:
Passo 2
Agora vamos fazer a somatória das forças em todos os eixos:
A somatória das forças em :
A somatória das forças em :
E as somatórias das forças em :
Passo 3
Agora vamos fazer a somatória dos momentos em todos os eixos, sabendo que não há resistência a momento na base do poste.
Somatória dos momentos em :
Agora fazendo a somatória dos momentos em :
Multiplicando por a primeira equação temos:
Somando as duas equações temos:
Logo será:
Passo 4
Agora basta substituir os valores das forças nos cabos para encontrar as reações na base:
Avançando:
E finalmente: