Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 28
28- Determine o momento de inércia polar e o raio de giração do triângulo isósceles mostrado na figura em relação ao ponto .
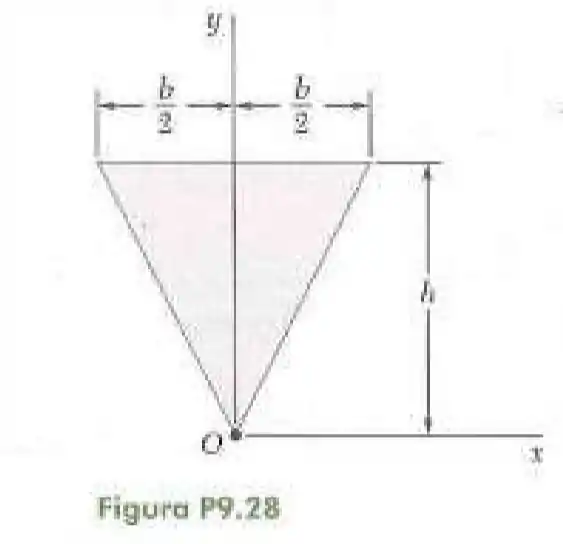
Passo 1
Dividindo a figura nos dois triângulos retângulos divididos pelo eixo (esses dois triângulos exercem a mesma inércia em e em ) e com isso podemos desenhar os elementos de área vertical e horizontal da seguinte maneira:
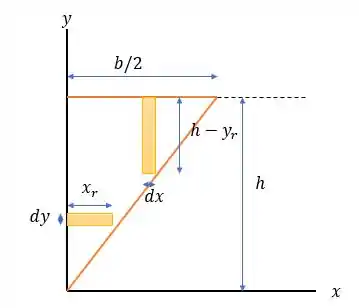
Onde e são as variáveis e da equação da reta diagonal e sabendo que essa reta passa pelos pontos e logo a reta terá equação igual a:
E
Então a equação da reta vale:
Essa seria e como isso será:
Então o elemento de área horizontal será igual a:
E o elemento de área vertical será:
Passo 2
Vamos calcular a área pelo elemento da área horizontal sabendo que varia de até . E que temos dois triângulos, nos dando a seguinte integral de área.
Dessa forma:
E com esse mesmo elemento de área nós podemos calcular a inércia em :
Não de esquecendo que temos dois triângulos e a linha horizontal considerando apenas um triângulo somente.
Passo 3
Agora para calcular a inércia em nós vamos utilizar o elemento de área vertical e nos dará:
Onde varia de até ou duas vezes a linha que vai de até .
Fazendo essa integral temos:
Dessa forma a inércia polar será igual a:
Passo 4
Como encontramos a área e a inércia polar então vamos encontrar o raio de giro polar: