Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 63

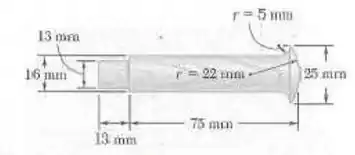
Um fabricante planeja produzir 20 . 000 cavilhas de madeira, como mostrado na figura. Determine quantos galões de tinta deverão ser pedidos, sabendo que cada cavilha leva duas demãos de tintas e que cada galão de tinta cobre 93 m 2 .

Passo 1

Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine quantos metros quadrados de tinta iremos precisar para pintar as cavilhas. Para isso, vamos calcular a área de uma cavilha através do Teorema de Pappus e utilizando figuras compostas. Logo, precisamos do comprimento do arco de cada uma dessas figuras e da distância percorrida pelo seu centroide:

x ¯ = ∫ a b x d A ∫ d A ;   y ¯ = ∫ a b y d A ∫ d A    

Primeiro, devemos determinar os termos x e y Para isso, devemos imaginar um retângulo de base infinitesival d x e altura y dentro da nossa função. Sendo assim, ficamos com:

x = x

y = y 2

Por último, vamos encontrar o termo d A , que é a área do nosso retângulo, ele é dado por:

d A = y . d x

Passo 2

Agora basta integrar no intervalo da função:

x ¯ = ∫ a b x d A ∫ d A

x ¯ = ∫ 25 a x y   d x ∫ 25 a y d x

x ¯ = ∫ 25 a x 1 x   d x ∫ 25 a 1 x d x

x ¯ = ∫ 25 a 1   d x ∫ 25 a 1 x   d x

Integrando, ficamos com:

x ¯ = x ​ 25 a ln ⁡ x ​ 25 a

x ¯ = a - 25 ln ⁡ a - ln ⁡ 25

Para y ¯ , basta repertimos o processo:

y ¯ = ∫ a b x d A ∫ d A

y ¯ = ∫ 25 a y 2   d x ln ⁡ a - ln ⁡ 25

y ¯ = 1 2 ∫ 25 a 1 x   d x ln ⁡ a - ln ⁡ 25

y ¯ = 1 2 ( ln ⁡ a - ln ⁡ 25 ) ln ⁡ a - ln ⁡ 25

y ¯ = 1 2

Substituindo na razão dada:

9 = a - 25 ln ⁡ a - ln ⁡ 25 1 2

9 2 = a - 25 ln ⁡ a - ln ⁡ 25

Resolvendo:

a = 98,79   m m

Resposta

a = 98,79   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume e a área da superfície do elo de corrente mostrado na figura, que é feito de uma barra de 6m m de diâmetro, se R = 10m m e L = 30m m .
Determine por integração direta os centroides das áreas a seguir.v
Determine o volume e a área da superfície do sólido obtido pela rotação da área da área do problema erm torno de ( a ) da linha y = 60 m m , ( b ) do eixo y .
Determine por integração direta os centroides das áreas a seguir.
Um arame homogêneo é dobrado na forma mostrada na figura. Determine por integração direta a coordenada x de seu centroide. Expresse sua resposta em termos de A .