29. O dispositivo é usado para manter a porta de um elevador aberta. Se a mola tem rigidez de e está comprimida em , determine os componentes horizontal e vertical da reação no pino e a força resultante no mancal da roda .
Passo 1
Primeiro, vamos ver o diagrama de forças da nossa situação, para analisar as reações que teremos que determinar no nosso sistema e ficar mãos simples de ver o que fazer.
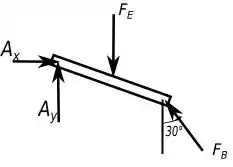
Então para achar as reações que o enunciado pede, teremos que usar as equações de equilíbrio.
Mas será mais conveniente calcular o momento em relação ao ponto , já quee , não interferem no cálculo do momento pois suas linhas de ação passam por .
Mas antes de começar a usar essas equações temos que achar a força que a mola faz no sistema, para isso temos que lembrar como é dada a força elástica, que é:
Onde é a constante elástica da mola e o deslocamento da mola, então pelos dados fornecidos no enunciado e pela figura, temos:
Passamos as distâncias para metros já que é o mais usado.
Vamos considerar o sentido anti-horário como o positivo.
Passo 2
Vamos então calcular o momento em relação a , para acharmos .
Passo 3
Agora vamos analisar as equações de equilíbrio referentes a força primeiro na direção , depois na direção .