69- O vínculo é utilizado para manter a barra no lugar. Determine a força axial no parafuso em necessária para que a maior força que deve ser aplicada na barra em ou seja de . Além disso, encontre a intensidade da força de reação no pino . Considere sem atrito todas as superfícies de contato.
Passo 1
Vamos separar o vínculo e analisar todas as forças que influenciam sobre ele.
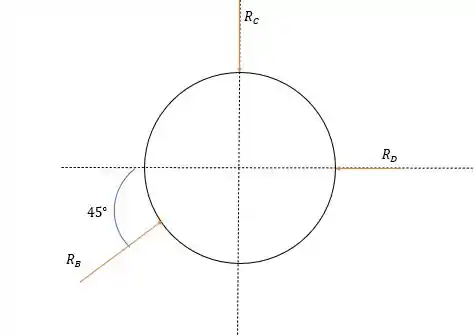
Fazendo a somatória das forças verticais temos:
E fazendo a somatória das forças horizontais:
Como o cosseno de é igual ao seno de então:
E como o enunciado diz que a maior força de será em uma das três reações logo essa força de 100 lb será a força . Logo:
Passo 2
Agora vamos analisar as forças na barra.
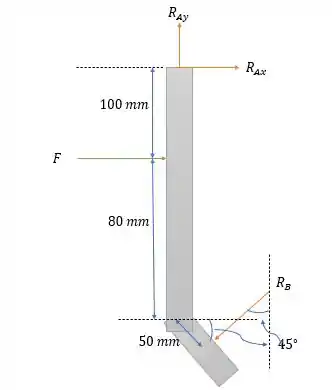
Onde é a força axial no parafuso e tem que ter sentido contrário a que foi considerada no vínculo.
Fazendo a somatória dos momentos em temos:
Onde temos que rebater a distância e a força na horizontal e na vertical para que possamos calcular o momento em .
Passo 3
Fazendo a somatória das forças verticais nós teremos:
E a somatória das forças horizontais será:
Logo a intensidade da força em será: