Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 30
30- Demonstre que o momento de inércia polar centoridal de uma dada superfície de área não pode ser menor que . (Dica: Compare o momento de inércia dada com o momento de inércia de um círculo com a mesma área e o mesmo centroide).
Passo 1
Considerando que esse círculo de comparação tem raio , então a inércia polar de um círculo é igual a:
E como a área de um círculo é:
Então a inércia em relação com a sua área terá uma fórmula igual a:
Porém com inventamos esse não é uma boa ter nenhum nessa fórmula logo uma outra forma de escrever é:
Pois isso dá no mesmo e ainda tira o da nossa fórmula.
Agora precisamos provar que independente da forma do corpo ele terá uma inércia maior que a de um círculo de mesma área.
Passo 2
Para isso vamos desenhar um corpo qualquer e o círculo de comparação.
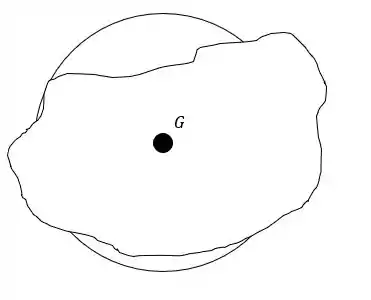
Ambas centradas em :
Para não perdemos o sentido da coisa vamos considerar a área que o corpo esquisito passa do perímetro do círculo igual a e a área que o círculo excede do perímetro do corpo igual a então podemos escrever a inércia polar do corpo da seguinte forma:
De forma um tanto simplificada temos essa análise:
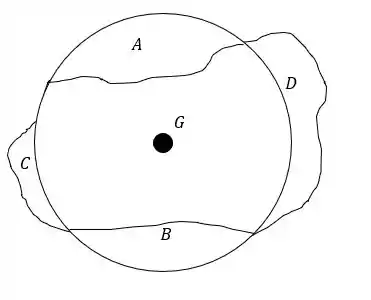
E se diminuirmos a área do círculo de e somarmos com nós teremos a área e a inércia do corpo.
Dessa forma:
Só que nos dá a inércia do círculo pois terá a mesmíssima área, como sobra a área externa ao perímetro do círculo então:
Então :
Resposta
Ei, a resposta está no passo a passo :)