Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 31
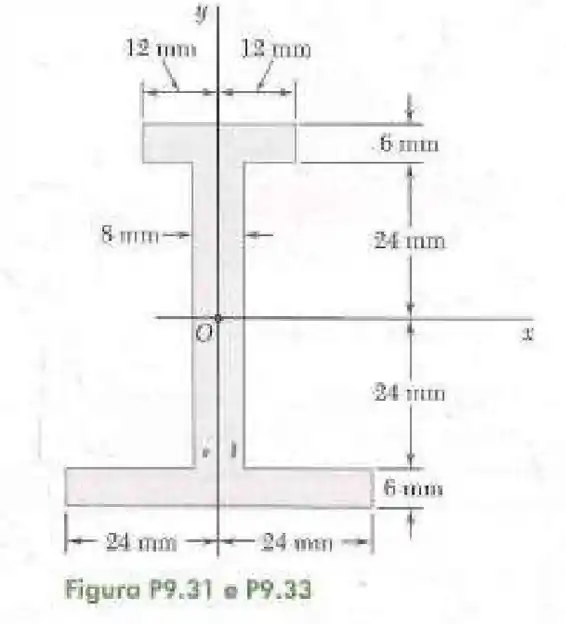
31- Determine o momento de inércia e o raio de giração da superfície sombreada em relação ao eixo .
Passo 1
A partir dessa seção nós estaremos mais preocupados em calcular a inércia de componentes bastante comuns na engenharia e como bons engenheiros que somos nós queremos praticidade ao extremo nas nossas contas, e integral não rima com praticidade mesmo então se faz necessário saber a inércia de certos elementos geométricos básicos como o retângulo que tem inércia igual a:
Onde é a base e a altura.
Inércia essa sendo calculada até o ponto de centro do retângulo. Qualquer dúvida você tem (ou deveria ter) condições teóricas de provar isso.
Dito isso vamos dividir a seção transversal da viga em três partes.
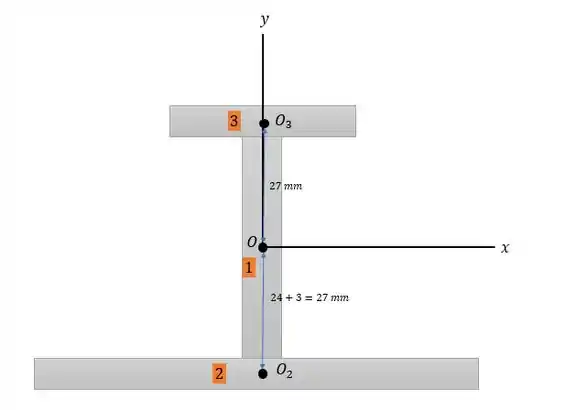
A região já nos dá a inércia em relação então não tem problema em fazer a inércia em nesse ponto:
Medida no
Passo 2
Agora para encontrar a inércia em das regiões em e nós precisamos fazer a inércia em relação a seus respectivos centros (distância essa em , para se ter o momento) e depois somar com multiplicação de suas áreas com a distância a ao quadrado.
Ou seja:
E:
O mais normal é errar conta aqui, então uma dica para não precisar fazer tudo isso é saber que , isso se você quiser fazer tudo no SI.
Então se somarmos todas as inércias nós teremos a inércia no corpo todo:
Passo 3
Como a área do corpo todo é a soma das áreas e logo:
Dessa forma o raio de giro em será: