Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 38

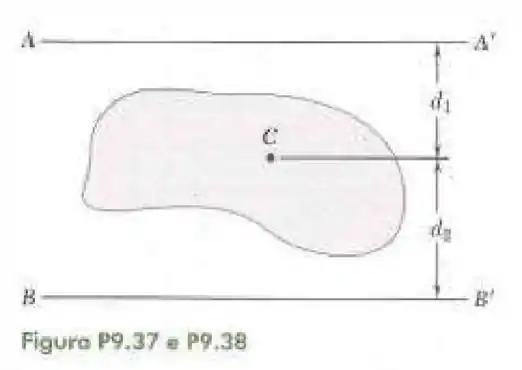
38- Determine para a superfície sombreada a área e o momento de inércia em relação ao eixo centroidal paralelo a B B ' , sabendo que d 1 = 25   m m e d 2 = 15   m m e que os momentos de inércia em relação a A A ' e B B ' são 7.84 × 10 6 m m e 5.20 × 10 6   m m 4 , respectivamente.

Passo 1

Sabendo que a inércia no eixo A A ' se correlaciona com a inércia no centro da seguinte forma:

I A A ' = I C + d 1 2 A

E com isso podemos isolar a área da seguinte forma:

A = I A A ' - I C d 1 2

A mesma coisa pode ser feita com a inércia no eixo B B ' nos dando:

A = I B B ' - I C d 2 2

Igualando as duas equações nós temos:

I A A ' - I C d 1 2 = I B B ' - I C d 2 2

Isolando I C (que caso não tenha entendido é a inércia no centro) nós teremos:

I B B ' - I C = d 2 2 d 1 2 I A A ' - I C

I C = I B B ' - d 2 2 d 1 2 I A A ' - I C

I C - d 2 2 d 1 2 I C = I B B ' - d 2 2 d 1 2 I A A '

I C = I B B ' - d 2 2 d 1 2 I A A ' 1 - d 2 2 d 1 2

Substituindo tudo nós temos:

I c = 5.20 × 10 6 - 15 2 25 2 7.84 × 10 6 1 - 15 2 25 2 = 3.715 × 10 6   m m 4

Passo 2

Substituindo os valores agora na equação da área nós temos:

A = I A A ' - I C d 1 2

A = 7.84 × 10 6 - 3.715 × 10 6   25 2 = 6600   m m 2

Resposta

I c = 3.715 × 10 6   m m 4

A = 6600   m m 2

Ver Outros Exercícios desse livro