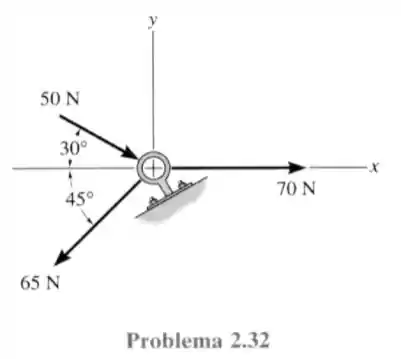
32- Determine a intensidade da força resultante e sua direção, medida no sentido horário a partir do eixo positivo.
Passo 1
E aí pessoal? Vamos para mais uma questão aqui do nosso maravilhoso livro.
O importante aqui dessa questão é saber projetar as forças nos dois eixos ordenados. Uma vez que a resultante dessas forças pode ser entendida como:
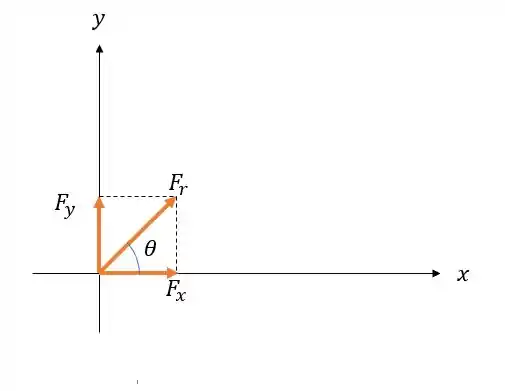
E a projeção dessa força resultante no eixo é chamado de e a projeção em é chamado de . E para realizar essas projeções nós fazemos:
E assim como a força resultante é a soma vetorial de todos os vetores, a nossa será a soma de todas as forças projetadas no eixo da seguinte forma:
Lembrando que a força de projetada no eixo aponta para o sentido negativo de , por isso o sinal negativo
O mesmo vale para a força , fazendo então a soma de todas as forças projetadas em
Uma vez que a força de projetada em é nula pois
Como a força em é negativa logo o ângulo da força resultante está no quarto quadrante. Pois a força resultante em é positiva e a força resultante em é negativa, no ciclo trigonométrico isso representa o quarto quadrante.
Passo 2
Beleza calculamos as orientações da força mas a questão nos pede a intensidade da força resultante, e ela pode ser calculada fazendo:
Passo 3
E a questão também pede o ângulo desse vetor resultante em relação ao eixo e para fazer isso nós fazemos:
Fazendo o arco tangente temos:
Então podemos entender a força resultante da seguinte forma:
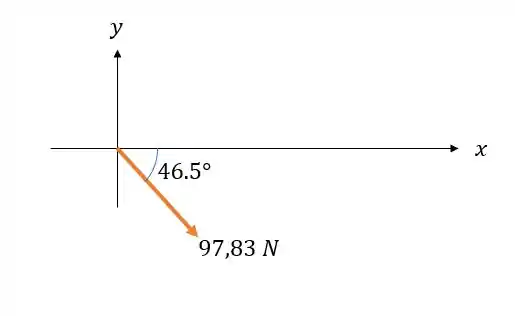
Onde esse ângulo respeita o ciclo trigonométrico padrão, que é no sentido anti-horário. Mas como a questão pede a direção (ou orientação) no sentido horário então invertemos o sinal.
E assim fechamos mais uma questão, vamos para mais uma!