Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.4 - Ex. 39

39- Expresse F 1 e F 2 como vetores cartesianos.

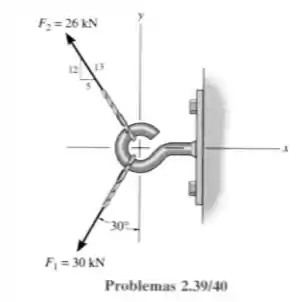
Passo 1

O cosseno e o seno do triângulo retângulo da força F 1 será:

cos ⁡ θ = 5 13

sin ⁡ θ = 12 13

Passo 2

A força F 2 projetada na horizontal fica:

F 2 x = 26 × cos ⁡ θ k N = 26 × 5 13 k N = 10   k N

Como o sentido da força está contra o do eixo x , logo:

F 2 x = - 10   k N

E em y :

F 2 y = 26 × sin ⁡ θ   [ k N ] = 26 × 12 13   k N = 24   k N

Logo em coordenadas cartesianas temos:

F 2 → = - 10 i ^ + 24 j ^   [ k N ]

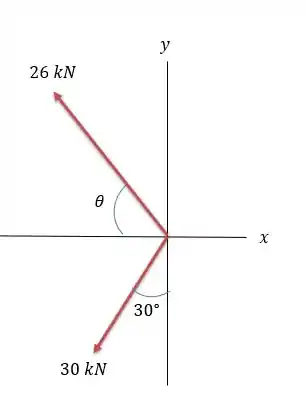
Passo 3

Agora a força F 1 projetada na horizontal é:

F 1 x = - 30 × sin ⁡ 30 = - 15   k N

Uma vez que na horizontal o sentido da força é o contrário do sentido do eixo x então:

Agora na vertical temos:

F 1 y = - 30 × cos ⁡ 30 = - 25.98   k N

Então em coordenadas cartesianas temos:

F 1 = - 15 i ^ - 25.98 j ^   [ k N ]

Resposta

F 1 = - 15 i ^ - 25.98 j ^   [ k N ]

F 2 = - 10 i ^ + 24 j ^   [ k N ]

Ver Outros Exercícios desse livro