Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 32

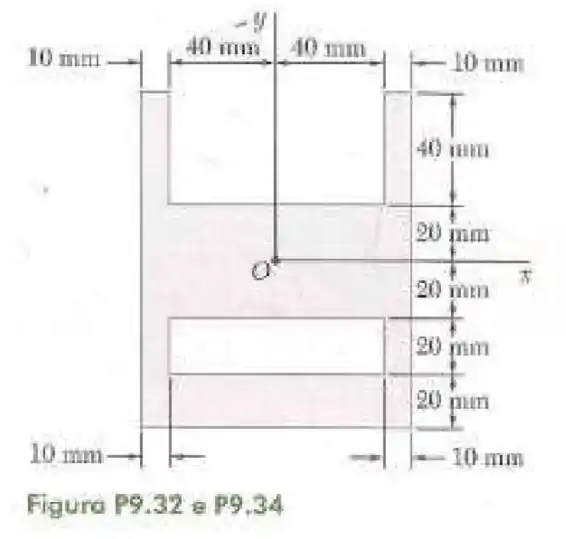
32- Determine o momento de inércia e o raio de giração da superfície sombreada em relação ao eixo x .

Passo 1

Existem diversas formas de se dividir essa ... ‘’coisa’’ aí, mas a forma mais didática para se explanar nesse momento aqui é da de fazer a inércia do retângulo inteiro, isso é com base de 100   m m e altura de 12 0   m m e tirar a inércia de dois retângulos inexistentes um com base de 80   m m e altura de 20   m m e outro retângulo de base de 80   m m e altura de 40   m m tal como pode ser visto abaixo.

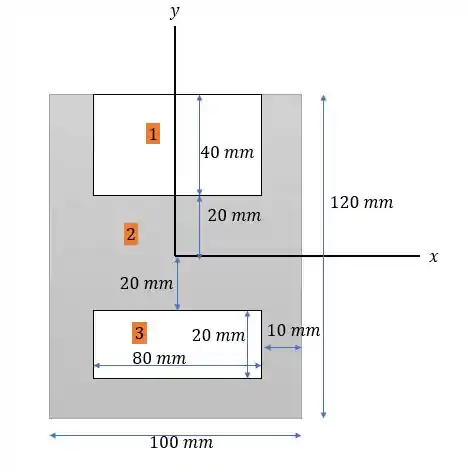
A área dessa superfície é igual a:

A = A 2 - A 1 - A 3

A = 120 × 100 × 10 - 6 - 40 × 80 × 10 - 6 - 20 × 80 × 10 - 6 = 7.2 × 10 - 3 m 2

Passo 2

E para calcular a inércia é a mesma essência , você diminui a inércia das áreas dos retângulos que não existem.

Sabendo que a inércia de um corpo em x no centro é calculado por :

I x = b h 3 12

A inércia da região 2 é calculado por:

I 2 x = 100 × 120 3 × 10 - 12 12 = 1.44 × 10 - 5   m 4

E a inércia da região 1 em relação a origem será:

I 1 x = 80 × 40 3 × 10 - 12 12 + 80 × 40 × 40 2 × 10 - 12 = 5.547 × 10 - 6   m 4

Pois a distância entre O e o centroide do retângulo 1 em y vale 20 + 40 2   m m .

E a inércia da região 3 :

I 3 x = 80 × 20 3 × 10 - 12 12 + 80 × 20 × 30 2 × 10 - 12 = 1.493 × 10 - 6   m 4

Dessa forma a inércia em x será igual a:

I x = I 2 x - I 1 x - I 3 x = 7.36 × 10 - 6   m 4

Passo 3

Dessa forma o raio de giração em x será igual a:

k = I x A

k = 7.36 × 10 - 6 7.2 × 10 - 3   = 31.97 × 10 - 3   m

Resposta

I x = 7.36 × 10 - 6   m 4

k = 31.97 × 10 - 3   m

Ver Outros Exercícios desse livro