Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 44

44- Determine os momentos de inércia I x e I y da superfície mostrada na figura em relação aos eixos centroidais paralelo e perpendicular ao lado A B , respectivamente.

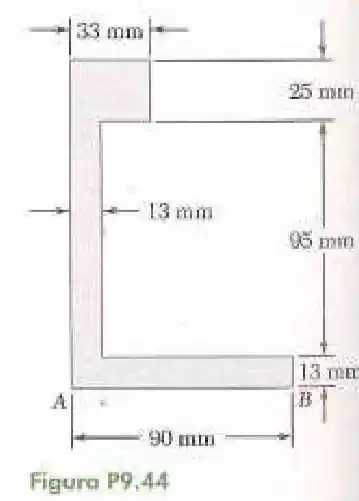
Passo 1

A figura pode ser dividida da seguinte forma:

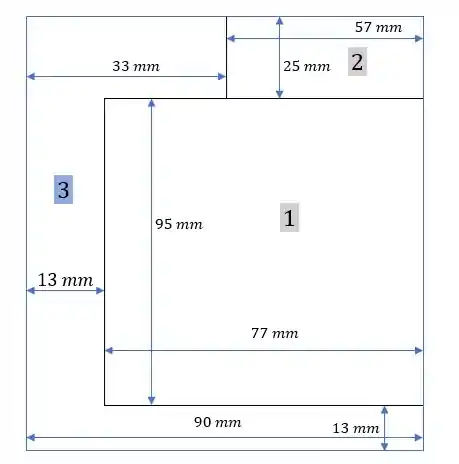
Onde a área 3 é a do retângulo todo.

Vamos encontrar o valor de centro em x e em y sabendo que eles tem a seguinte fórmula:

y ¯ = ∑ y A ∑ A ;       x ¯ = ∑ x A ∑ A

E eles serão:

y ¯ = y 3 ¯ A 3 - y 2 ¯ A 2 - y 1 ¯ A 1 A 3 - A 2 - A 1                   x ¯ = x 3 ¯ A 3 - x 2 ¯ A 2 - x 1 ¯ A 1 A 3 - A 2 - A 1

E por termos muitas formas geométricas vamos fazer uma tabela com os valores:

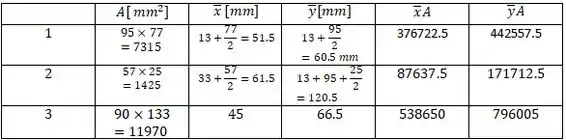
Logo :

y ¯ = 796005 - 442557.5 - 171712.5 11970 - 1425 - 7315 = 56.26   m m

x ¯ = 538650 - 87637.5 - 376722.5 11970 - 1425 - 7315 = 23   m m

Passo 2

A inércia em x será calculada por:

I x = I 3 x - I 2 x - I 1 x

E por serem retângulos a inércia em relação a seu centro será:

I x = b h 3 12 + A d 2

Distância essa sendo em y .

Isso será:

I 3 x = 90 × 133 3 12 + 90 × 133 66.5 - 56.26 2 = 18.9 × 10 6   m m 4

I 2 x = 57 × 25 3 12 + 57 × 25 120.5 - 56.26 2 = 5.95 × 10 6   m m 4

I 1 x = 77 × 95 3 12 + 77 × 95 60.5 - 56.26 2 = 5.63 × 10 6   m m 4

Então a inércia será:

I x = 7.32 × 10 6   m m 4

Passo 3

E a inércia em y :

I y = I 3 y - I 2 y - I 1 y

E a inércia em y com retângulos será calculado por:

I y = b 3 h 12 + A d 2

Dessa forma nós queremos a distância em x :

I 3 y = 90 3 × 133 12 + 90 × 133 45 - 23 2 = 13.87 × 10 6   m m 4

I 2 y = 57 3 × 25 12 + 57 × 25 61.5 - 23 2 = 2.5 × 10 6   m m 4

I 1 y = 77 3 × 95 12 + 95 × 77 × 51.5 - 23 2 = 9.56 × 10 6   m m 4

Dessa forma a inércia em y será:

I y = 1.81 × 10 6   m m 4

Resposta

I x = 7.32 × 10 6   m m 4

I y = 1.81 × 10 6   m m 4

Ver Outros Exercícios desse livro