Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.4 - Ex. 33
33- Determine a intensidade da força , de modo que a resultantente das três seja a menor possível.
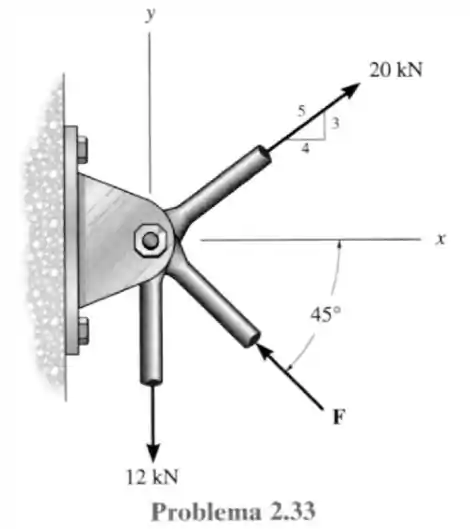
Passo 1
Sabendo que o cosseno e o seno do triângulo retângulo retratados na figura podem ser calculados por:
Isso é a parte horizontal precisará multiplicar por e a vertical por .
Então temos a seguinte somatória das forças horizontais:
E para a somatória das forças verticais temos:
Valores das forças em .
Passo 2
Logo o módulo da intensidade da força resultante será:
Substituindo os valores que encontramos no passo anterior temos:
Logo a equação da força resultante será:
Passo 3
Como o termo que acompanha é positivo logo a equação do segundo grau tem concavidade apontando para cima, sendo uma equação que tem um mínimo local, que pode ser encontrado fazendo a equação:
Fazendo a derivada pela regra da cadeia temos:
Para essa equação ser zero o numerador da equação tem que ser zero. Logo: