Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 35

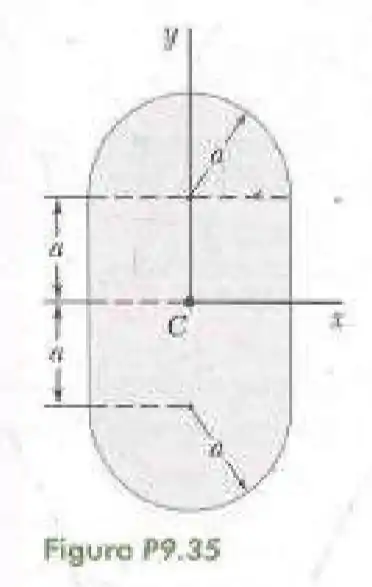
35- Determine os momentos de inércia da superfície sombreada mostrada na figura em relação aos eixos x e y quando a = 20   m m

Passo 1

Vamos dividir a figura em três regiões, os dois semicírculos de raio a e o quadrado de raio 2 a .

Começando pela inércia no quadrado nós temos:

I x = I y = 16 a 4 12 = 4 a 4 3

Pois é em relação ao centro.

E as inércias nos semicírculos seriam iguais a:

I x = 2 × π a 2 2 × a + 4 a 3 π 2 + π a 4 8

I y = 2 × π a 4 8 = π a 4 4

Passo 2

Logo a inércia total no corpo será:

I y = 4 a 4 3 + π a 4 4

I x = 4 a 4 3 + π a 4 4 + π a 2 a + 4 a 3 π 2

Então para a = 20   m m teremos:

I x = 1.36 × 10 6   m m 4

I y = 339 × 10 3   m m 4

Resposta

I x = 1.36 × 10 6   m m 4

I y = 339 × 10 3   m m 4

Ver Outros Exercícios desse livro