Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 39
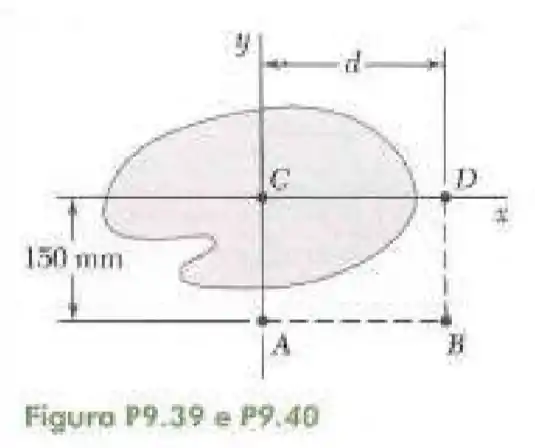
39- A área sombreada é igual a . Determine os momentos centroidais de inércia e sabendo que e que o momento de inércia da área sobre o ponto é .
Passo 1
O momento de inércia polar está ligado como o momento de inércia polar no centro da seguinte forma:
Dessa forma o momento de inércia polar no centro valerá:
Substituindo os valores nós temos:
Passo 2
E como o momento polar no centro pode ser escrito da seguinte forma:
E como , logo:
Então:
Então: