39- O trabalhador usa um carrinho de mão para levar material rampa abaixo. Se o carrinho e seu conteúdo são mantidos na posição mostrada, ambos pesando , com o centro de gravidade em , determine a força normal resultante das duas rodas no solo em e a intensidade da força necessária na mão do trabalhador em .

Passo 1
O mais complicado dessa questão é o desenho mesmo, e ele está abaixo.
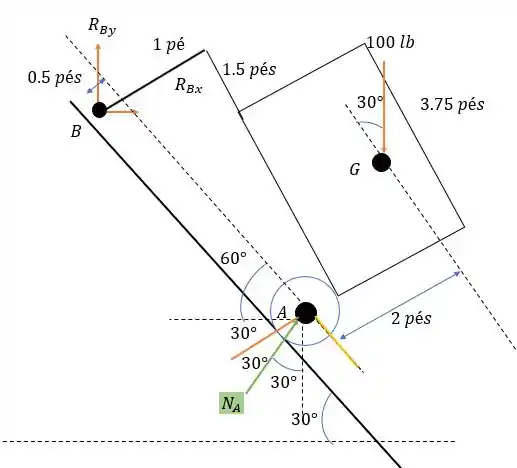
Passo 2
Vamos encontrar primeiro a força de reação nas rodas fazendo a somatória dos momentos em .
Onde temos que rebater na reta laranja (que é normal a reta paralela a rampa ) e para a reta amarela que é paralela a rampa) com o intuito de encontrar o momento em . Com isso encontramos:
Passo 3
Agora fazendo a somatória das forças verticais e horizontais encontraremos a resultante em na mão do cara.
Fazendo a somatória das forças verticais:
Agora para a somatória das forças horizontais:
A resultante será igual a: