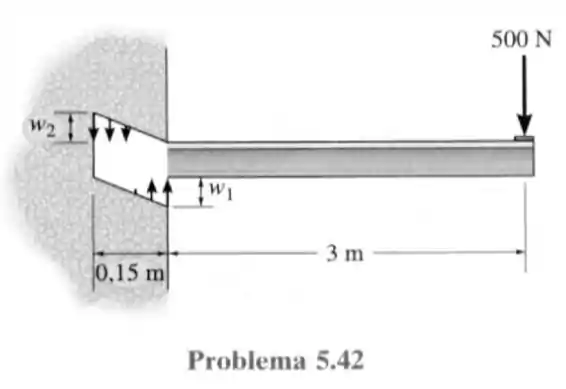
42- Uma viga em balanço, com comprimento livre de , é submetida a uma força vertical de , conforme a figura. Supondo que a parede resista a essa carga com uma distribuição linear de cargas numa extensão de na porção embutida da viga, determine a intensidade dos carregamentos distribuídos e para manter o equilíbrio.
Passo 1
A figura dada pode não ter ficado muito clara, por isso vamos redesenhar-la aqui.

A carga que aponta para baixo que tem máximo de tem uma força resultante igual a:
E está distante do ponto em:
E a carga que aponta para cima com máximo igual a tem uma força resultante igual a:
E está distante do ponto em:
Passo 2
Isso nos dá uma viga equivalente igual a:

Fazendo a somatória das forças verticais temos:
E agora fazendo a somatória dos momentos em :
Passo 3
Resolvendo esse sistema:
Logo: