Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 40

40- O momento polar de inércia da área sombreada com relação a A , B e D são, respectivamente, J A = 1.125 × 10 6   m m 4 ,   J B = 2.625 × 10 6   m m 4 e J D = 1.782 × 10 6   m m 4 . Determine a área sombreada, seu momento de inércia centroidal J C e a distância d para C e D .

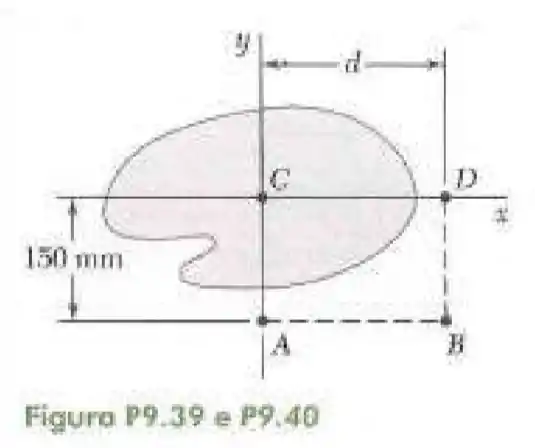
Passo 1

Escrevendo o momento de inércia polar em relação a A nós temos:

J A = J C + A d A C 2

Isso é:

1.125 × 10 6 = J C + 150 2 A

Agora a equação da inércia em relação a B será:

J B = J C + A d C B 2

Onde por Pitágoras vemos que:

d C B 2 = 150 2 + d 2

Logo:

2.625 × 10 6 = J C + A ( 150 2 + d 2 )

Agora escrevendo a inércia em relação a D temos:

J D = J C + A d C D 2

O que nos dá:

1.782 × 10 6 = J C + A d 2

Passo 2

Diminuindo a segunda equação da terceira temos que:

2.625 - 1.782 × 10 6 = 150 2 A

O que nos dá:

A = 37.46   m m 2

Passo 3

Dessa forma se substituirmos esse valor de A na primeira equação nós teremos:

1.125 × 10 6 = J C + 37.46 × 150 2

J C = 0.28215 × 10 6   m m 4

Passo 4

E substituindo esses valores na terceira equação temos:

1.782 × 10 6 = 0.28215 × 10 6 + 37.46 d 2

d = 200   m m

Uma forma de verificar a resposta, é colocar esses valores em todas as equações , você achará as inércias em cada ponto com um erro mínimo.

Resposta

A = 37.46   m m 2

J C = 0.28215 × 10 6   m m 4

d = 200   m m

Ver Outros Exercícios desse livro