Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 42
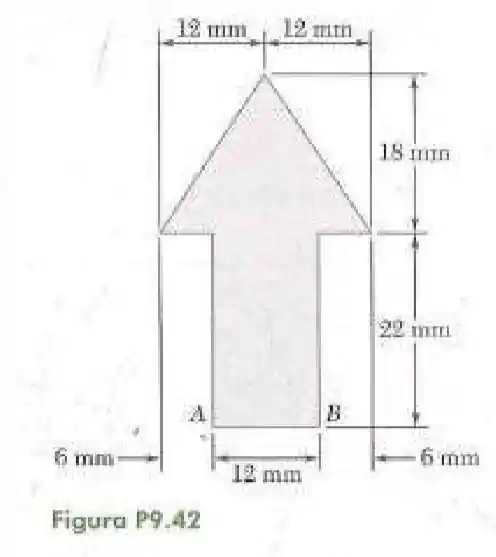
42- Determine os momentos de inércia e da superfície mostrada na figura em relação aos eixos centroidais paralelo e perpendicular ao lado , respectivamente.
Passo 1
Como o eixo está na horizontal na superfície isso nos dá a possibilidade de traçar o eixo na horizontal rente a esse eixo. Fazendo isso e dividindo o corpo em dois nós teremos a seguinte figura.
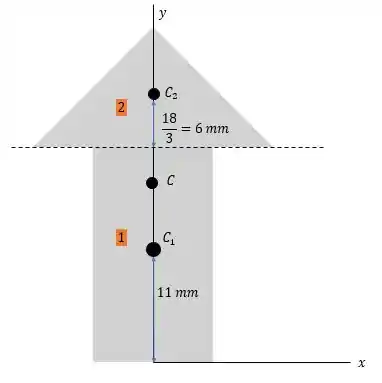
Para que seja possível fazer essa inércia em relação ao seu centro nós precisamos descobrir a posição ... do centro da figura toda haha e para isso temos os centros do retângulo (área 1) e do triângulo (área 2). E para achar esse valor vamos fazer a seguinte conta:
Passo 2
Começando pela inércia em no centro dessa figura:
Onde:
Isso será:
E:
Isso será:
Então a inércia no centro em será:
Passo 3
Agora para a inércia em no seu centro.
Onde :
Como as duas regiões tem centroides na mesma posição horizontal então não há o termo .
Então:
E para calcular o momento em no triângulo vamos fazer a moda antiga:
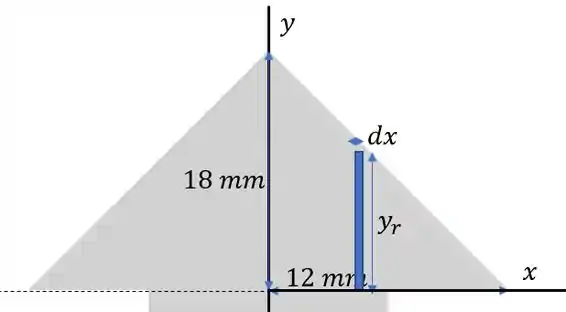
Onde é o da reta e que passa pelos pontos e :
Logo a equação da reta será:
E o elemento de área vertical será:
Como temos dois triângulo e varia de até nós temos a seguinte integral:
Dessa forma a inércia no centro em no corpo todo será: