40- A viga está sujeita as duas cargas concentradas, como é visto na figura. Supondo que a base da fundação exerce uma distribuição de cargas que varia linearmente, determine as intensidades das cargas e na condição de equilíbrio em função dos parâmetros mostrados na figura e faça os cálculos com , .

Passo 1
Basicamente a questão quer que a gente encontre os valores de e em função de e de forma genérica e depois utilizando valores.
Vamos traçar um eixo e dividir a carga em duas áreas para que seja possível resolver essa questão.
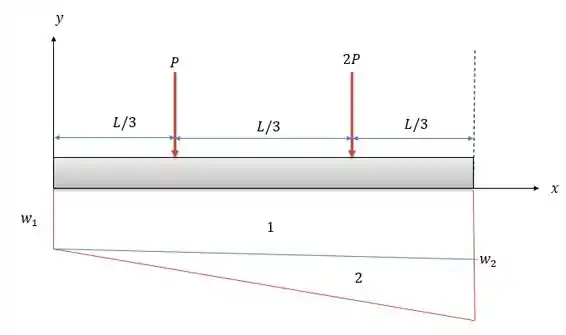
A área retangular produz uma carga na barra igual a:
E encontra-se em uma posição em relação a origem igual a:
Enquanto a carga triangular produz na barra uma força resultante igual a:
Pois é a área do triângulo
E essa força resultante se situa no centro de área desse triângulo que está em:
Passo 2
Isso faz com que o sistema de forças esteja da seguinte maneira:
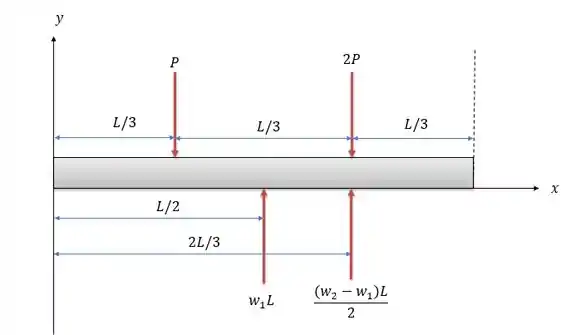
Se fizermos a somatória das forças verticais nos sistema nós teremos:
Agora fazendo a somatória dos momentos em relação a origem nós teremos:
Cortando e passando os que tem sinal negativo para o outro lado nós teremos:
Passo 3
Resolvendo o sistema temos:
Diminuindo o segundo pelo primeiro:
Logo:
Passo 4
Para a letra b queremos que seja e seja então:
Resposta
a)
b)