53- A barra uniforme tem peso de e a mola está relaxada para . Determine a rigidez da mola para de modo que a barra fique em equilíbrio.
Passo 1
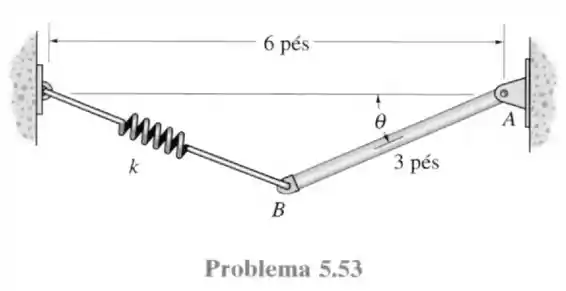
Vamos desenhar o triângulo formado entre as paredes, a mola e a barra.

Pela lei dos cossenos conseguimos ver que o comprimento final da mola será igual a:
E conseguimos ver que em a mola tem um comprimento inicial igual a:
Isso nos diz que a variação do comprimento será igual a:
Pela lei dos senos conseguimos encontrar :
Porém como o outro lado vale , então obrigatoriamente é um ângulo maior que .
Passo 2
Feita a parte geométrica vamos calcular a força na mola desenhando o diagrama de forças, sabendo que o apoio resiste a forças verticais e horizontais:
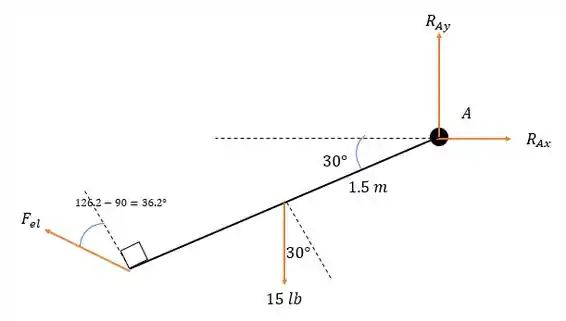
Fazendo a somatória dos momentos em temos:
Passo 3
Logo a rigidez da mola será calculado por: