Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 47
47- Determine o momento de inércia polar da área mostrada na figura em relação ao ponto , ao centroide da superfície.
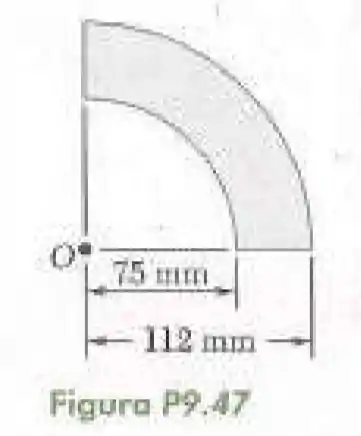
Passo 1
Vamos encontrar o centroide dessa superfície dividindo a superfície no quarto de círculo de raio igual a menos o quarto de círculo de raio igual a . Tendo assim a fórmula de e .
E o cálculo da inércia polar em nos daria:
Passo 2
Para calcular a inércia polar no centroide nós temos que saber a distância entre e (a linha reta que liga os dois pontos ) e ela será calculada por:
E essa inércia será calculada pela seguinte fórmula:
Dessa forma (que será a inércia polar no centroide) será: