Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.4 - Ex. 22
Determine o momento de cada uma das três forças em relação ao ponto A. Resolva o problema primeiro utilizando cada força como um todo e, depois, o princípio dos momentos.
Passo 1
E aii gurizada tudo bem? Antes de começarmos os cálculos vamos começar esquematizando o problema para melhor facilitar o entendimento...
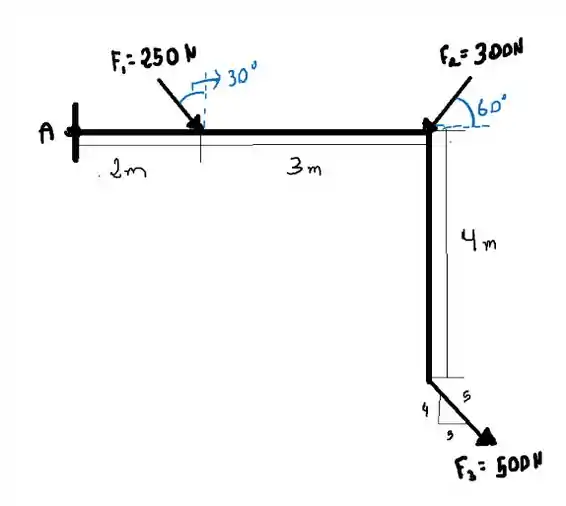
Repare que as distâncias serão as medidas perpendiculares entre o ponto A e a força
Vamos calcular isso logo
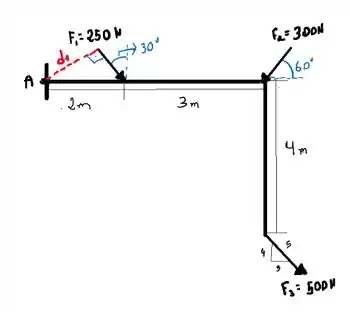
Primeiramente vamos calcular , mas antes vamos lembrar da trigonometria básica, olhem:
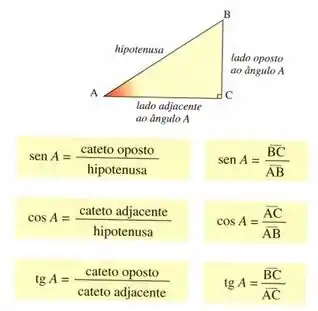
De maneira análoga para encontrarmos temos a seguinte esquematização...
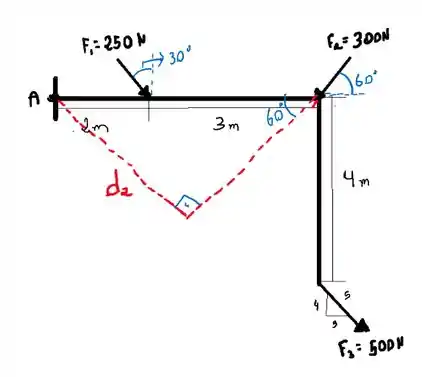
Vamos determinar o ângulo de pelo triângulo
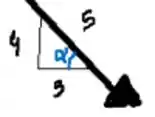
Então
Logo
De maneira análoga para encontrarmos D3 temos a seguinte esquematização...
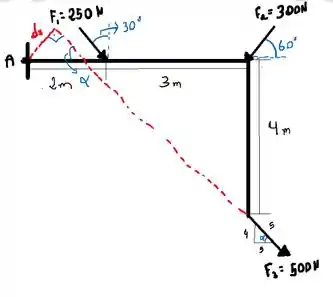
Passo 2
Agora que já temos todas as forças e todas as distâncias, é só lembrar que:
Então temos:
Ou
No sentido horário.
Ou
No sentido horário.
E por fim
Ou
No sentido horário
Passo 3
Vamos agora fazer o que o enunciado pede e calcular tudo de novo, mas agora usando o principio dos momentos.
A grande diferença é que não usaremos a distância perpendicular, mas vamos decompor as forças em termos de x e y, vamos lá, lembrando que:
Ou
No sentido horário.
Ou
No sentido horário.
E por fim
Basta usar aquele triângulo que usamos pra determinar , lembra?
Ou
No sentido horário
Resposta
No sentido horário.
No sentido horário.
No sentido horário.