4.28. Determine a direção , com , da força F, de maneira que ela produza (a) o máximo momento em relação ao ponto A e (b) o mínimo momento em relação ao ponto A. Calcule o momento em cada caso.
Passo 1
Vamos começar esquematizando o problema
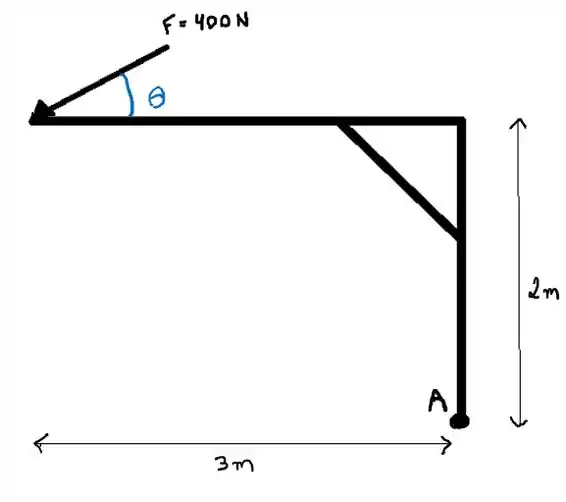
Passo 2
Vamos começar pensando no maior momento. Para o momento ser máximo a distancia até o de A até o ponto onde a força está sendo aplicada devem ser perpendiculares. Então teremos esse triângulo.
O momento então será
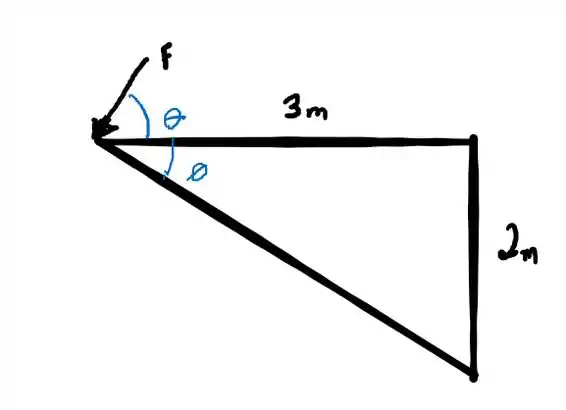
Podemos determinar
Então
Logo
Passo 3
Agora vamos analisar o momento mínimo.
O momento mínimo deve ser 0, então
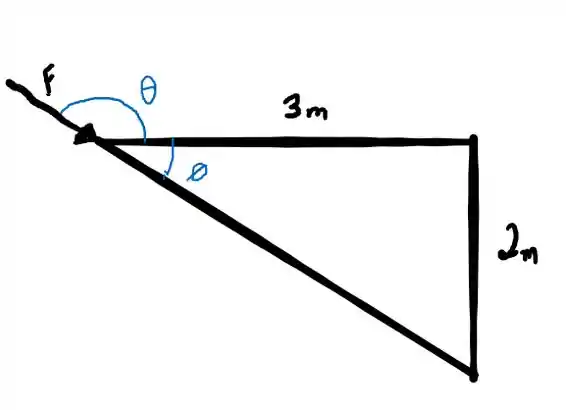
A força deve ser paralela a distância, então teremos a relação
Já sabemos o ângulo , então basta fazer