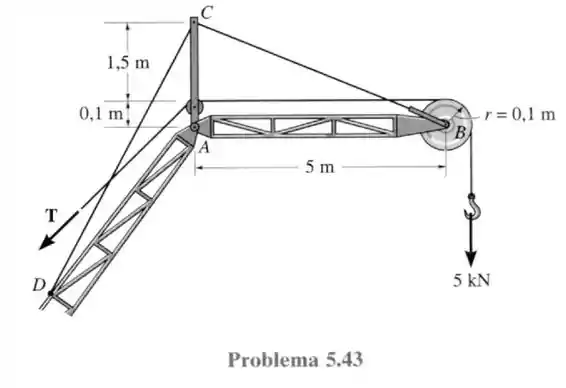
43- A parte superior da lança do guindaste consiste da estrutura , que é apoiada pelo pino em , pelo seu cabo de sustentação e pelo cabo que sustenta o mastro em . Cada um desses cabos está ligado independentemente ao mastro. Determine a intensidade da força resultante que o pino exerce na estrutura em para a condição de equilíbrio, a tensão no cabo e a tensão no cabo elevador, quando a carga de está suspensa por esse cabo, que pela polia em . Despreze o peso da estrutura . A polia em tem raio de .
Passo 1
Analisando as forças na polia conseguimos ver que pela somatória dos momentos no centro da polia que:
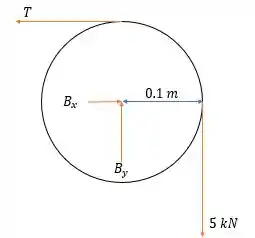
Além de que pela somatória das forças na horizontal que:
E pela somatória das forças verticais que:
Passo 2
Agora vamos traçar o sistema de forças na lança .
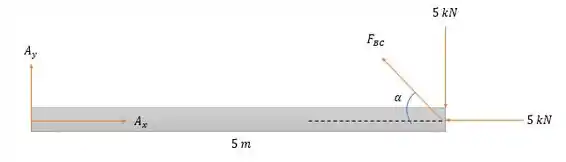
Onde vale:
Tem que se considerar o valor de uma vez que o cabo sai do centro da polia e por ação e reação as forças da polia entram com sentido contrário na lança.
Fazendo a somatória dos momentos em temos:
Passo 3
Agora podemos encontrar as reações em fazendo a somatória das forças horizontais e verticais na lança.
Fazendo a somatória das forças horizontais:
E a somatória das forças verticais:
Logo o módulo da força vale: