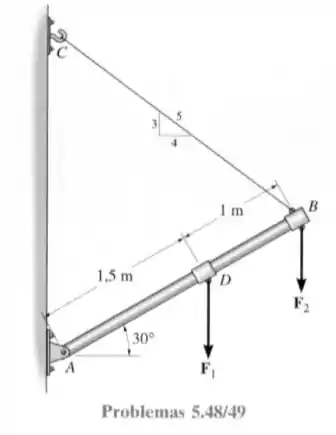
49- A lança da figura deve manter penduradas duas cargas verticais e . Se a carga máxima suportada pelo cabo é de , determine as cargas críticas para a condição . Qual é a intensidade da reação máxima no pino ?
Passo 1
Dessa vez foi dado a força e pede-se agora as forças e , o sistema de forças continuará o mesmo mas o calculo será o inverso agora.
Passo 2
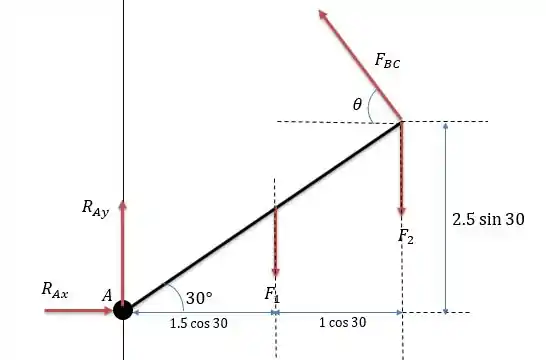
Adotando que e que temos a seguinte somatória dos momentos em .
Dessa forma:
Então será:
Passo 3
Para calcular o módulo da reação no pino precisamos saber as componentes vertical e horizontal nesse pino, para isso vamos fazer primeira a somatória das forças horizontais.
E agora a somatória das forças verticais:
E o módulo será calculado como: