4.33. Segmentos de um tubo D para perfuração de um poço de petróleo estão ajustados por meio de uma pinça reguladora T que aperta o tubo e de um cilindro hidráulico (não mostrado na figura), para regular a força F aplicada à pinça. Essa força atua ao longo do cabo que passa ao redor de uma pequena polia P. Estando o cabo originalmente perpendicular à pinça, como mostrado na figura, determine a intensidade da força F que deve ser aplicada de modo que o momento em relação ao tubo seja . Com o intuito de manter esse mesmo momento, qual intensidade de F é necessária quando a pinça é ajustada em 30°, como na posição esboçada com tonalidade mais clara? Nota: o ângulo DAP não é 90° nessa posição.
Passo 1
Vamos começar esquematizando o problema
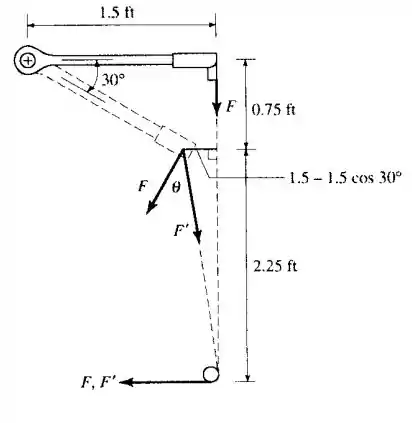
Essa questão é meio complicadinha de interpretar, mas o grande truque é sacar essa força F’ agindo sobre a pinça reguladora, ela se refere a segunda parte do problema. Ela aparece porque sabemos que se a componente perpendicular a pinça de F’ for igual a F, o ângulo vai se manter o mesmo.
Passo 2
O momento como sabemos é mas também é , então
Aqui tiramos que
Passo 3
Lembra que falei do F’? pois bem, ele vai ser útil agora
Lembre-se que queremos manter o mesmo momento, então a componente da força perpendicular a pinça deve se manter igual.
Agora esse pode ser calculado da seguinte maneira
Logo temos