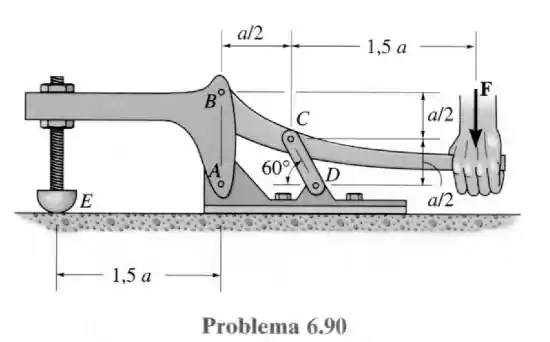
90- O cabo da prensa de alavanca articulada está sujeito a uma força . Determine a força de prensagem vertical que atua em .
Passo 1
Podemos desprender o corpo do cabo (corpo onde se segura e que passa pelos pontos e ) do corpo onde se aplica a prensagem (corpo ). O que nos dá o seguinte diagrama de forças.
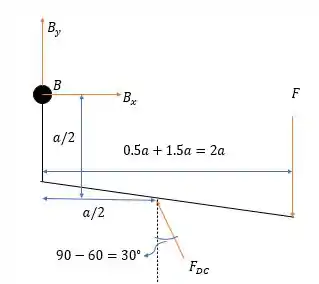
Onde temos a força de ação da barra atuando, logo se fizermos a somatória dos momentos em nós teremos:
Agora vamos fazer a somatória das forças para encontrar as forças de reação em .
Fazendo a somatória das forças horizontais nós temos:
E fazendo a somatória das forças verticais:
Passo 2
Agora vamos fazer o diagrama de forças no corpo da prensadora, onde agora destacando esse corpo deveremos inverter o sentido de reação no pino e colocar as reações no pino .
Isso nos dá:
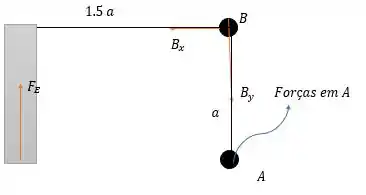
é o nome que demos para força que faz a prensa.
A somatória dos momentos em será igual a: