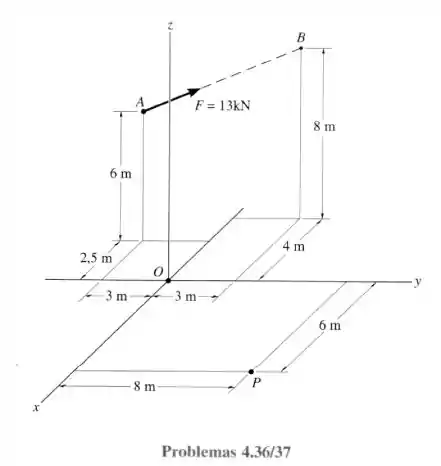
4.36. Determine o momento da força F em A relativamente ao ponto O. Expresse o resultado como um vetor cartesiano.
Passo 1
Falaaa... beleza???
Pra achar o momento do vetor F:
E vai ser “só” isso...
Mas vamos identificar quais são os pontos A, B e O porque vamos precisar...
Passo 2
Vamos começar reparando que tudo é vetor na equação, então vamos achar esses vetores antes, aí:
- Para o :
Só pra ficar bonitinho... =X
Passo 3
- para o : (vetor)
Atençãozinha aqui porque nos foi dado o módulo dessa força (), mas a gente pode ver que a setinha está em cima do vetor unitário .
Pro vetor, então:
Uma pausinha pra achar :
Voltando:
Passo 4
Calma que vamos agora pra última parte... Já ta acabando...
Calculando momento, então:
Ufaa.. acabamos... Partiu pra próxima???