46-O guincho da figura consiste em um tambor de raio de , que está conectado por pinos no seu centro em . Na sua parte exterior há uma catraca com raio médio de . A lingueta atua como um elemento de duas forças (haste curta) e bloqueia a rotação do tambor. Determine os componentes horizontal e vertical da reação no pino , sabendo que a carga suspensa pesa .
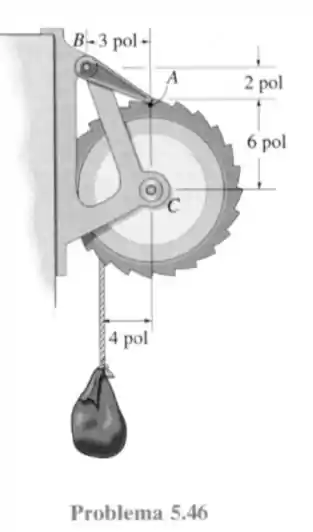
Passo 1
A questão nos diz que o pino reage em dois eixos (vertical e horizontal) e a força na lingueta é a força paralela a esta, com isso podemos desenhar o sistema de forças da seguinte forma:
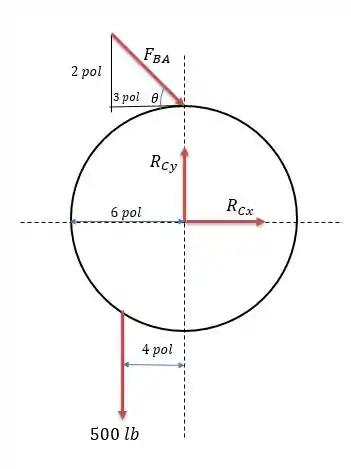
Onde na força vale:
Passo 2
Fazendo a somatória das forças no centro do círculo nós iremos encontrar:
Onde a projeção vertical de não gera momento no centro do círculo, por estar no mesmo sentido que o eixo vertical do círculo. Logo:
Passo 3
Com o valor de conseguimos encontrar o valor das reações em fazendo a somatória das forças verticais e horizontais:
Fazendo a somatória das forças horizontais temos:
Isso significa que o sentido da força está ao contrário do que desenhado.
Fazendo agora a somatória das forças verticais temos: