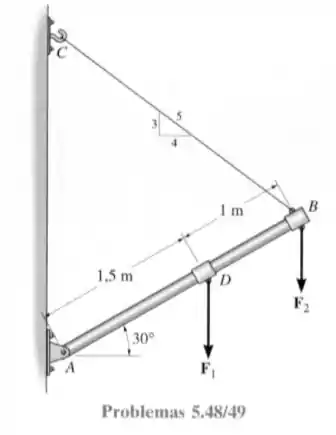
48- A lança mantém penduradas duas cargas verticais. Despreze as dimensões dos colares em e , a espessura da lança e calcule os componentes horizontal e vertical da força no pino e a força no cabo . Considere e .
Passo 1
O pino em resiste a forças tanto na horizontal quanto na vertical o que nos faz desenhar o sistema de forças da seguinte maneira.
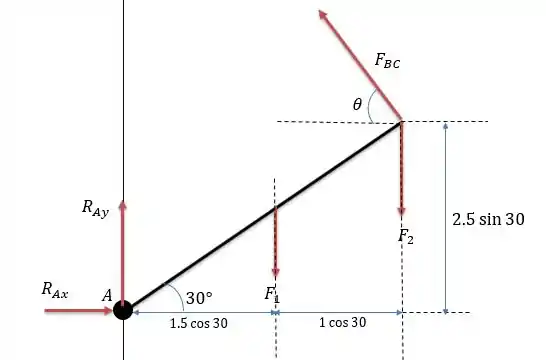
De modo que tem as seguintes relações trigonométricas.
E temos as seguintes projeções horizontais do eixo para a força até a origem e da força até a origem, além da projeção vertical de até a origem, essas projeções serão importante para calcular o momento em relação a .
Passo 2
Como e temos então o cálculo de fazendo a somatória dos momentos até .
Substituindo todos os valores temos:
Onde gera momento em se projetando-a na vertical e na horizontal.
Passo 3
Agora para encontrar a reação vertical e horizontal no apoio basta fazer a somatória das forças verticais e horizontais e igualar a zero, com isso fazendo a somatória das forças verticais temos:
E o somatória das forças horizontais nos dá: